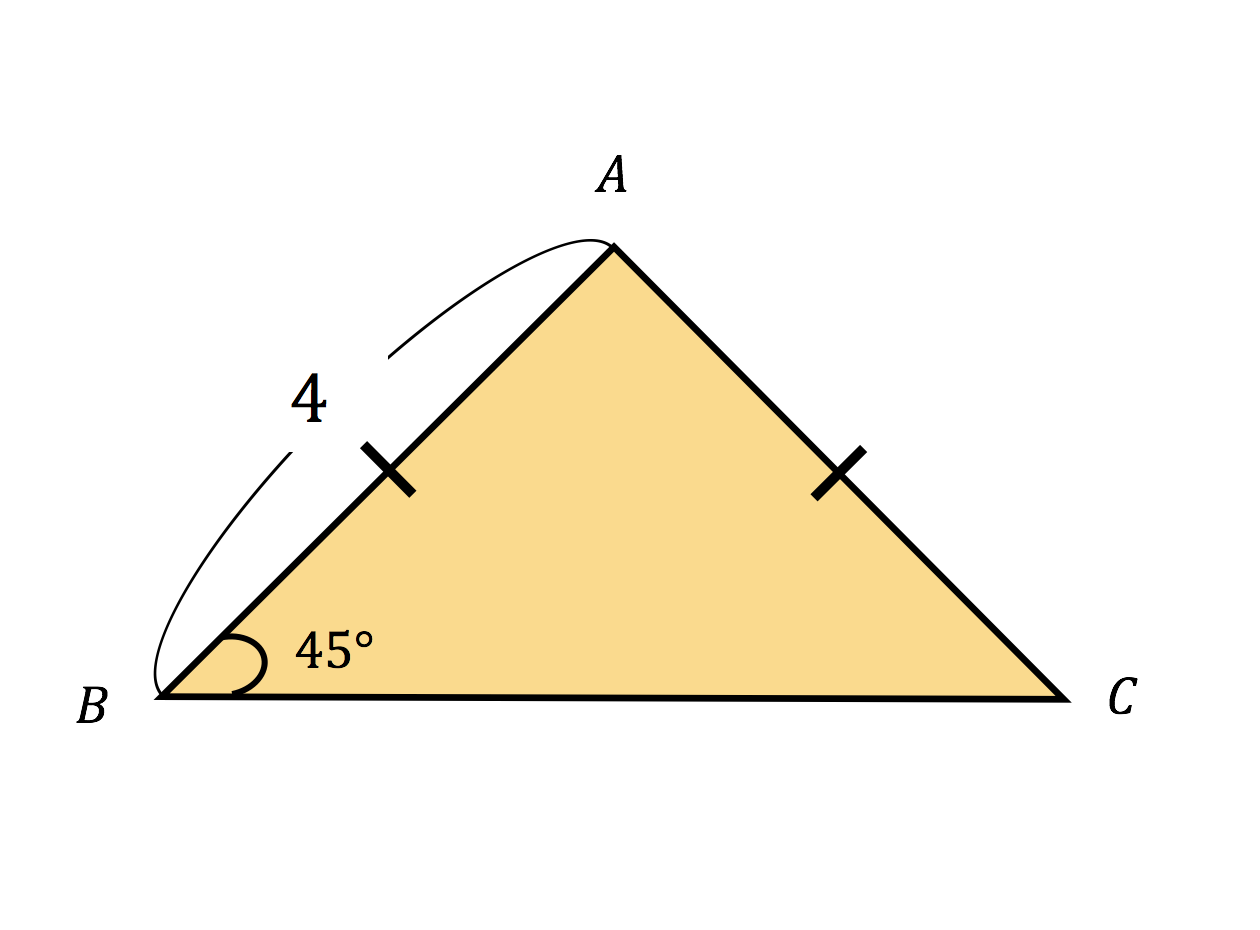
直角二等辺三角形 (ちょっかくにとうへんさんかくけい、 英 isosceles right triangle )は、 二等辺三角形 の持つ特徴に加え、 直角三角形 の持つ特徴を併せ持つ 図形 である。 3つの 角 のうち2つの角がそれぞれ45°である三角形と定義してもよい。 図1のように、15°の直角三角形の線分比はになります。これを証明するために、図2のように、まずはAC=1として考え始めます。 ①60°の直角三角形ADCができるようになるように補助線を引く ABD二等辺三角形になるので、 ②BCに対称な三角形ができるように点A'をとる ③図3のように∠acb=1°に着目し、その外角の60°を使って特別な直角三角形を作る。 d 60° 4 4 3 11 頂点aからbcの延長線上に垂線をおろし交点をdとする。 ≫ すると acdが30°60°90°の直角三角形になるので 辺の比を使ってad,cdの長さを出す。 8ad=2 3 2ad=8 3 ad=4 3 8cd=21 2cd=8 cd=4 ≫
Mathematics 三平方の定理 2 特別な直角三角形 働きアリ
直角 二 等辺 三角形 比
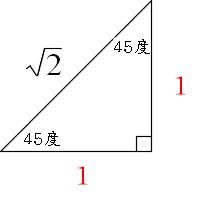
直角 二 等辺 三角形 比-はしご直角三角形(二等辺直角三角形) 三角形だから、 辺が3つ あるよね。これが、 それぞれ等しければ 、合同だと言えるんだよ。 この場合、角度についてわかっていなくても大丈夫なんだ。直角二等辺三角形の辺の長さの比は 1 1 √2 でしたから、 と分かります。三平方の定理の応用 三平方の定理が成り立つ整数の組 三平方の定理は、平方が登場してくる関係上どうしてもルートが出てきやすくなってしまいます。 その




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
特別な直角三角形 ① 直角二等辺三角形 ② 30 °,60 °,90 °の直角三角形 11 2:: 132:: ③ 整数比の辺をもつ直角三角形 345:: :: ②の30 °,60 °,90 °の角をもつ直角三角形は,正三角形を1 つの中線で切 り分けたときにできる図形です。基本的な三角形と三角比 正方形の半分 直角二等辺三角形(各辺の比は 1 1 2) sin 45 ° = BC AB = 1 2 cos 45 ° = AC AB = 1 2 tan 45 ° = BC AC = 1 1 正三角形の半分 各辺の比が 1 2 3 の直角三角形 sin 30 ° = BC AB = 1 2 cos 30 ° = AC AB = 3 2 tan 30 ° = BC AC = 1 3 sin 60 ° = AC AB = 3 2 ∠ABOは、正三角形のひとつの角なので60°、よって∠BAOは30°。 つまり ABOは、30°、60°、90°という3つの角で構成された直角三角形であることがわかります。 この直角三角形は、三辺の比が\(1:2:\sqrt{3}\) になる特別な図形です。そのため、高さは\(3\sqrt{3}cm\) 。
①は、BC=ACの直角二等辺三角形で、 と辺の比がきまっています。つまり、仮にa=1cmだった場合、b=1cm、c=√2cmに、a=2cmだった 直角二等辺三角形の辺の求め方 直角二等辺三角形の底辺が106センチメートルの場合、底辺じゃない辺の長さって何センチになりますか? 直角二等辺三角形は二等辺三角形の一つでもあり、直角三角形の一つでもある。 等しい長さの2辺で構成される1角 (頂角)が 直角 である。 斜辺 どうしが重なり合うように二つの直角二等辺三角形を並べると 正方形 ができる。第25回 三角比を使う NHK;
直角二等辺三角形比, 直角二等辺三角形の辺の長さは?1分でわかる求め方、 直角二等辺三角形の辺の長さは?1分でわかる求め方、公式、辺の長さと角度の関係、証明 無料サンプルあり!一級建築士対策にも使えるお得な用語集はこちら⇒ 全77頁! 直角二等辺三角形 直角(90度)以外の二つの角度は45度 。 正三角形と直角三角形 正三角形はすべての角度が60°。 正三角形を半分にすると「30°、60°、90°の直角三角形」になり、 一番長い辺が一番短い辺の2倍の長さになる 。 三角形の面積の公式―底辺× 今、二等辺三角形が熱い! ~小学校の算数が懐かしい デイリーポータルZ 21年5月31日 自分が小学生時代に流行ったマンガやアニメ、おもちゃなどに触れると、懐かしむのみならず改めてハマってしまうことはないだろうか。 筆者は最近、で中学




高校数学 三角形の形状 正三角形 二等辺三角形 直角三角形 受験の月
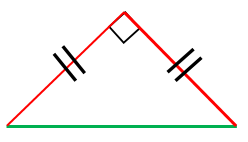



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
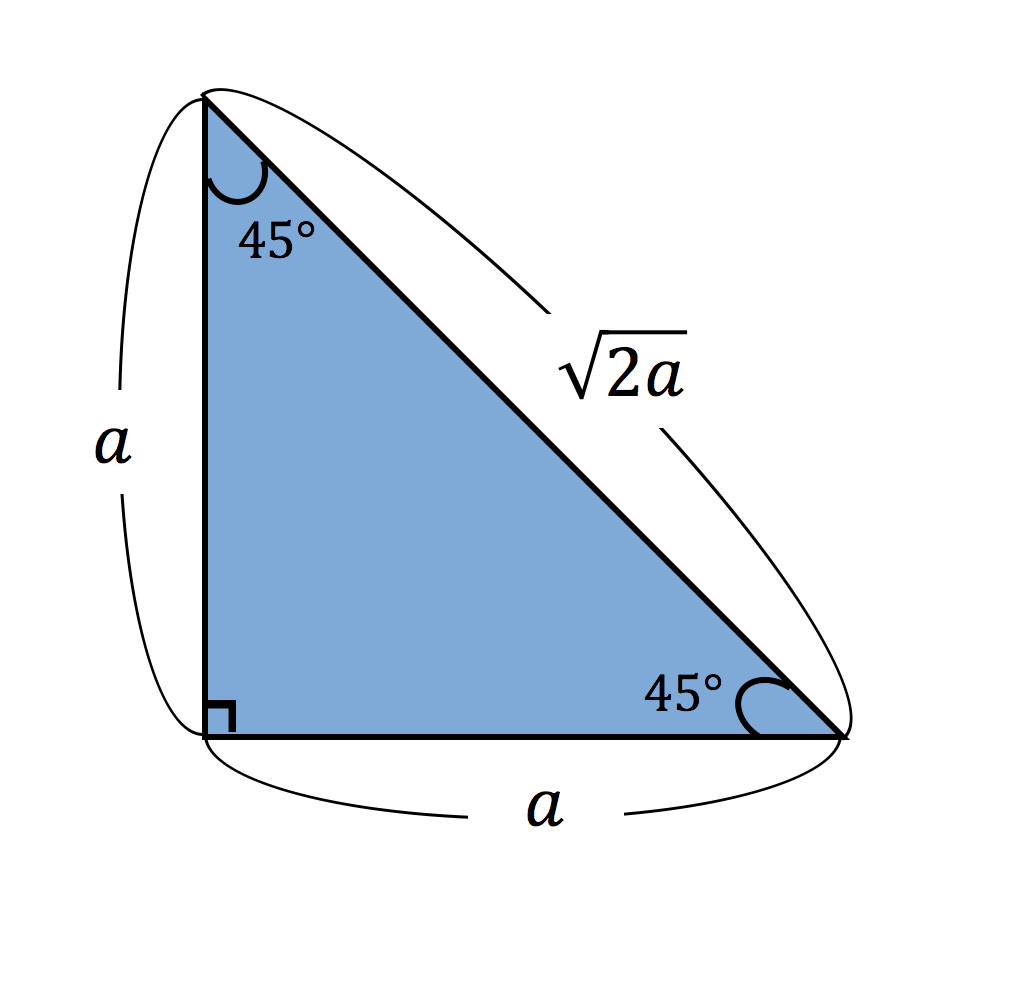
直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。直角二等辺三角形の2辺の長さがそれぞれ5だったとき、もう1辺の長さはどうなるでしょうか。 5 制作・著作/NHK (Japan Broadcasting Corp) このページに辺の長さの比1:1:√2 60°と30°の直角三角形です。 いちばん長い辺はいちばん短い辺の2倍の長さ です。 辺の長さの比1:2:√3



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
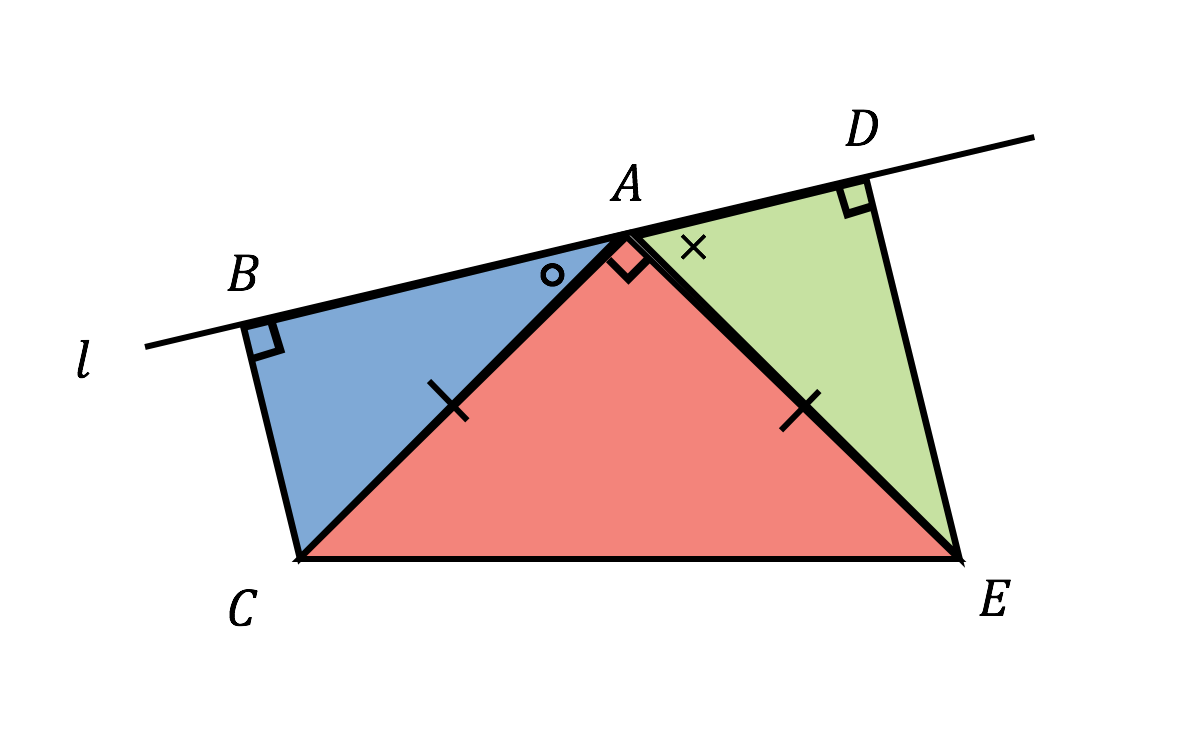
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な直角三角形2 右の図で PO は∠AOB の二等分線である。 ∠OAP=∠OBP=90°のとき AP=BP となることを証明しなさい。 A B O P 右の ABCで頂点Bから辺ACに垂線をおろし、その交点をEとする。 同様にCからABに垂線をおろしその交点をDとする。 BD=CEならば ABCは二等辺左の直角三角形は、正三角形を半分にしたものです。 \(3\) 辺の比は暗記で、\(21\sqrt{3}\) です。 よって、下の図のように長さが決まります。 \(x=3\sqrt{3}\) です。 右の直角三角形は、正方形を半分にした直角二等辺三角形です。




面積 直角二等辺三角形 小学4年生算数 そらいろ日記 言葉の宝箱



直角二等辺三角形befの面積は 2006年算数オリンピック ファイナル問題より 算数オリンピック問題に挑戦
直角二等辺三角形の定規の辺の比は、11 √2(内角は、90°、45°、45°) この場合、斜辺が√2です。 1² + 1² =√2² また、直角二等辺三角形といえば、正方形を対角線で半分に切った図形です。特別な直角三角形の辺の比 無料で使える中学学習プリント 直角二等辺三角形三角 25 × 25 × 354 m hdpe ネット帆ガーデンネット 95% シェーディング uv 保護直角二等辺三角形は 「30°、60°、90°」と「45°、45°、90°」の直角三角形の辺の比 関連:直角二等辺三角形の辺の長さの求め方 補足、まめ知識 ・「45°、45°、90°」の直角三角形の辺の長さの比を「$\sqrt{2}11$」や「$1\sqrt{2}1$」と言うこともできますが「$11



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
$15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。直角二等辺三角形 C言語で図形の面積を求めるプログラムの参考にさせていただきました。 計算式が書いてあるのが親切でいいと思いました。 私もあずま袋を縫いたくて計算しました。 やっぱり50×150がベストっぽい! 小鳥が餌を食べる為の囲いを作る三角形の相似条件について図解で分かる相似条件 直角二等辺三角形とは?定義や辺の長さの比、面積の求め方 二等辺三角形 Wikipedia 二等辺三角形の性質と辺の長さの求め方!押さえておきたい三



直角二等辺三角形の斜辺を三等分したら直角も三等分されますよね ならない Yahoo 知恵袋



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明
第233問 直角二等辺の辺の比 図形ドリル 直角三角形 直角二等辺三角形 相似 ★★★★★☆(算オリ・灘中受験生レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの直角二等辺三角形の辺の長さの比は1:1: 2 でしたね。 したがって, x :6 = 1: 2 から 2 x = 6 を解いて x = = = = 3 2第296問 辺の比と直角 図形ドリル 5年生 6年生 三角形 直角 辺の比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げて




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



直角二等辺三角形 Wikipedia
直角三角形の左端の角度が45度(直角二等辺三角形)の時の三角比は次のようになります。 1対1対√2で覚えてください。 この直角二等辺三角形を半分に折ると、同じ形 (相似) の直角二等辺三角形がで つまり、内角がそれぞれ90°、45°、45°の二等辺三角形の三辺の比は、1:1:√2となるのです。 公式 直角二等辺三角形の辺の長さの比:1:1:√2 この公式はかなりの頻度で利用する必要が生まれますので、是非とも覚えてしまうことをおすすめします。三角形の形状問題(正三角形,二等辺三角形,直角三角形など三角形の種類を言い当てる問題)や証明問題においては,正弦定理や余弦定理を変形して,角度に関する式を辺に関する式に直してから考えるのが原則です. ・ tan A は上記2つを用いてとします




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく
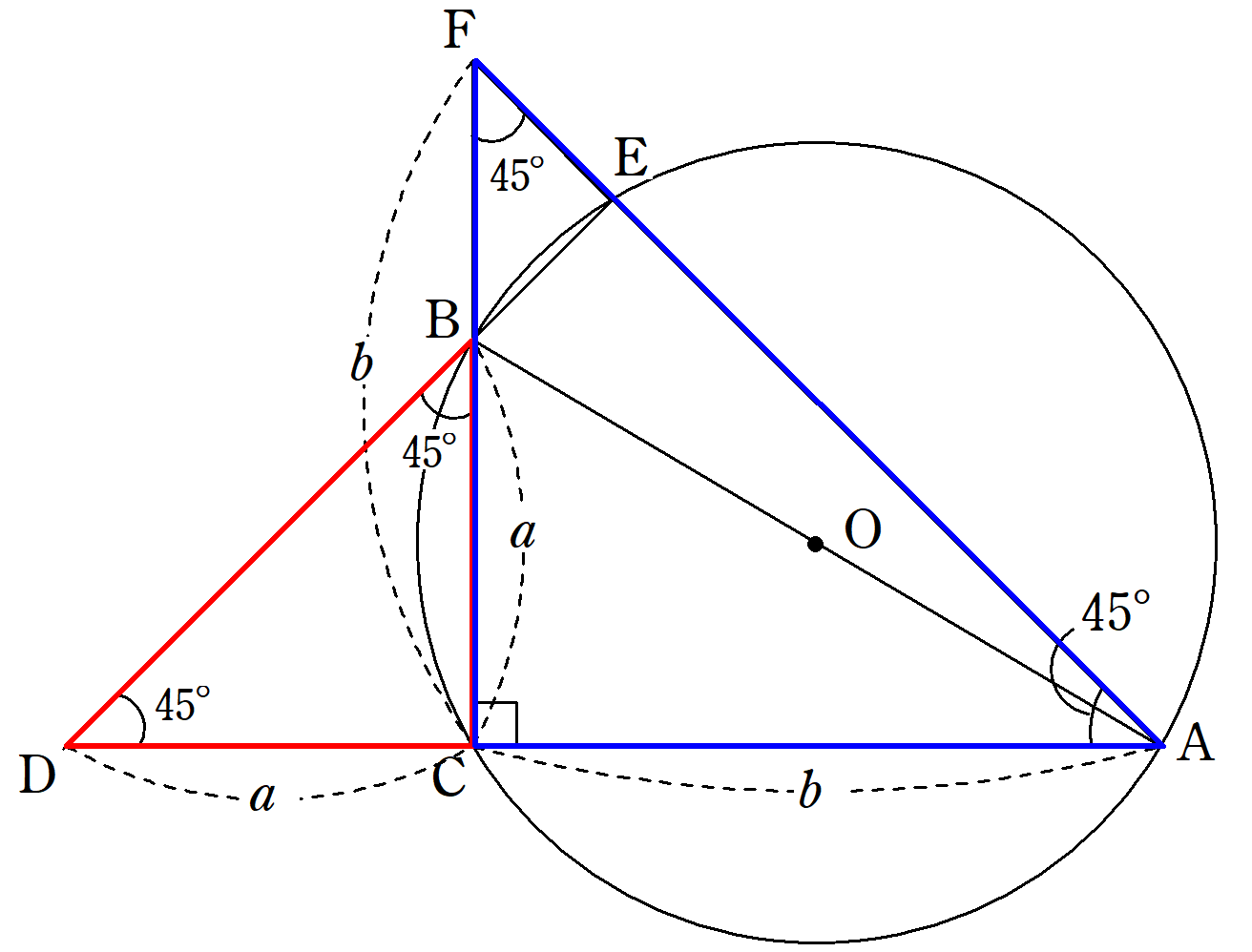



三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも




数学の内心の問題です 1 1 2の比の直角三角形の内接円の半径が1セン 数学 教えて Goo




1 はどうして二等辺三角形の辺の比1 1 2 を使えないんですか Clear



数学の質問です ルート2はどこから分かるんですか 直角二等辺三角 Yahoo 知恵袋



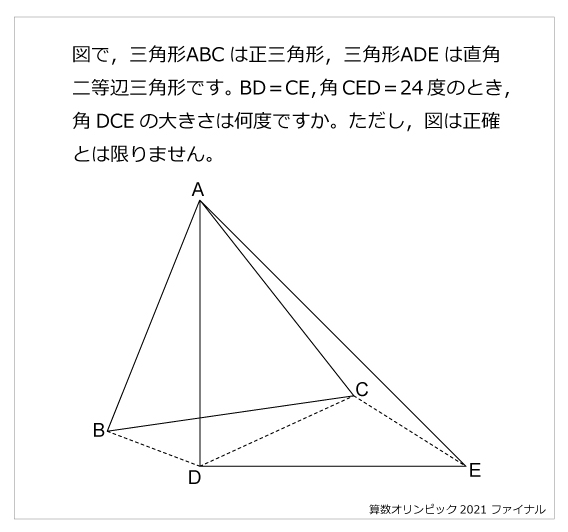
直角二等辺三角形の面積は 2006年算数オリンピック ファイナルより 中学受験ー算数解き方ポータル




なぜ三角形cdeは直角二等辺三角形だとわかるのかが理解できません 教えてください Clear
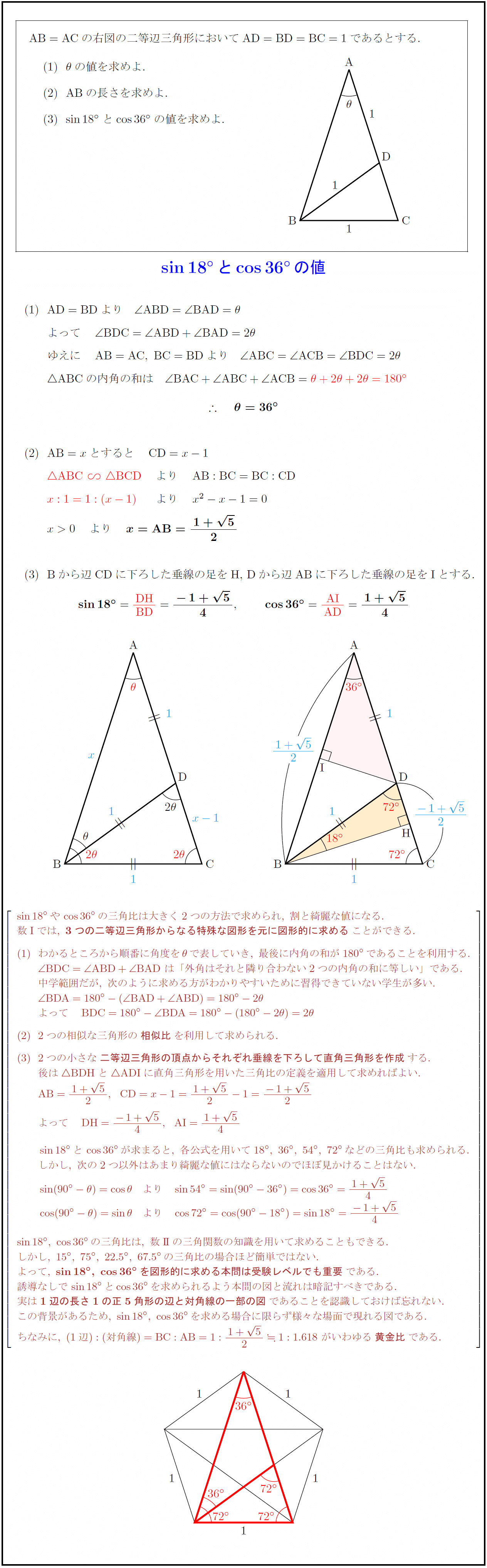



高校数学 Sin18 とcos36 の値 正五角形を利用した図形的解法 受験の月



直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題
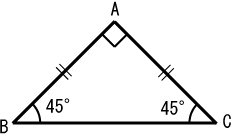



直角二等辺三角形 Wikipedia
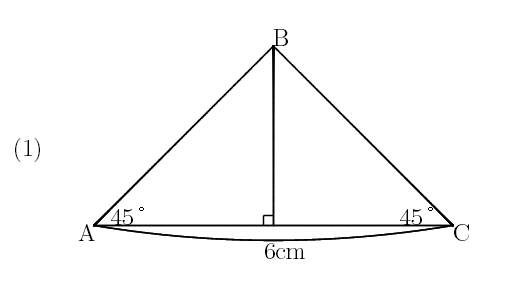



問題例 直角二等辺三角形の比の関係 図形 Mathpub1 Wiki Atwiki アットウィキ
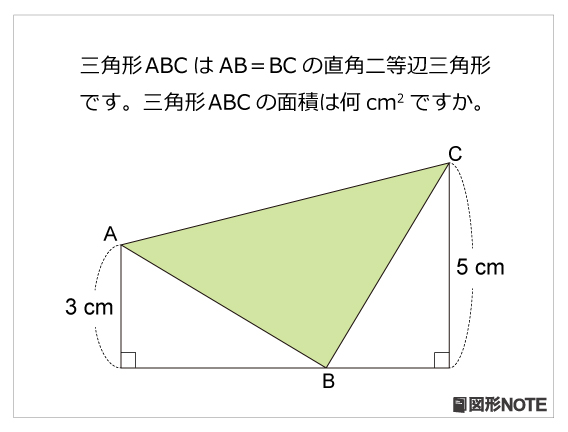



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



Perfume トライアングル 直角二等辺三角形 ある広告人の告白 あるいは愚痴かもね
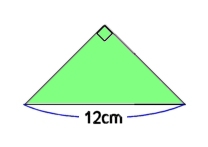



直角二等辺三角形



二等辺三角形の 3辺の長さの比率は同じですか 例えば 一番小さい角の角 Yahoo 知恵袋




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
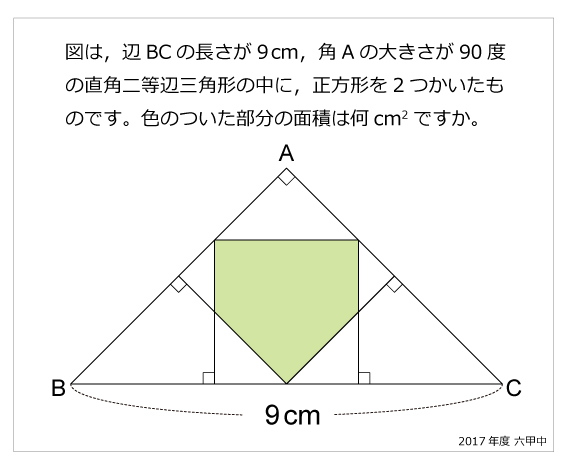



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
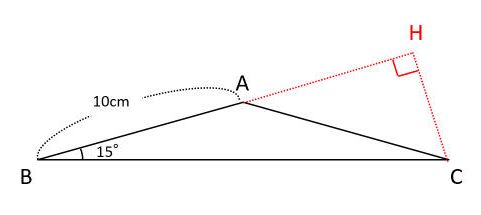



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




3 4 5の三角形で 本当に直角ができる Note Board
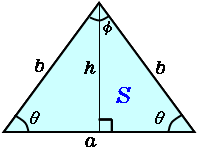



二等辺三角形 高精度計算サイト



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明



中学受験 算数 平面図形の問題です 直角二等辺三角形と直角三角形を図のように Yahoo 知恵袋
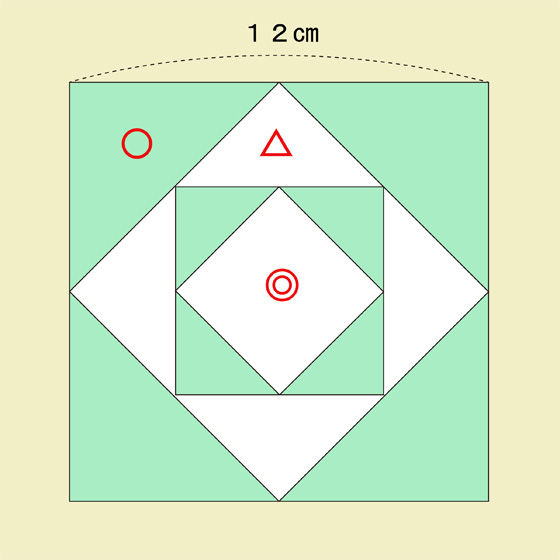



簡単に答えを出す方法に気付けるか 白い部分の面積を求める問題 秒刊sunday




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
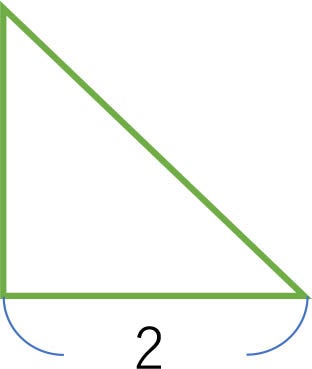



面積 直角二等辺三角形 小学4年生算数 そらいろ日記 言葉の宝箱




直角二等辺三角形の辺の求め方 直角二等辺三角形の底辺が106センチメ 数学 教えて Goo




直角二等辺三角形 ウィクショナリー日本語版
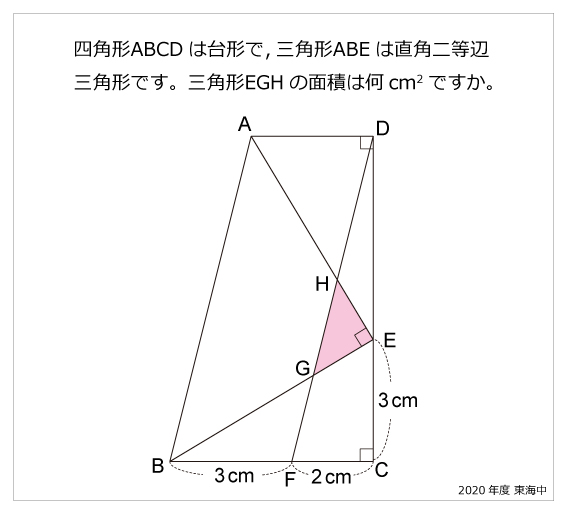



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1 1 ルート2 三角形




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




โน ตของ 確認 三平方の定理 直角二等辺三角形 ช น Senior Clear




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく
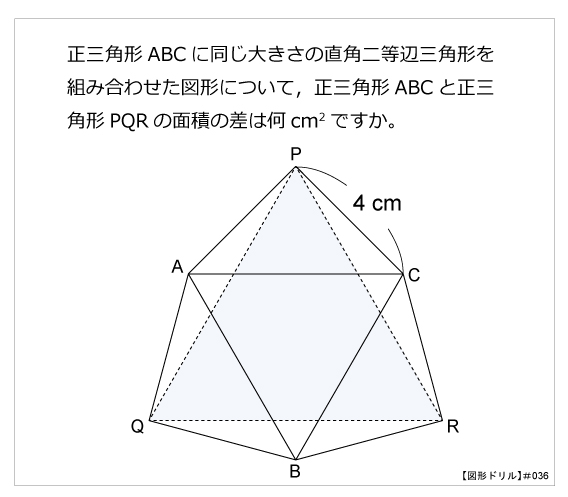



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo
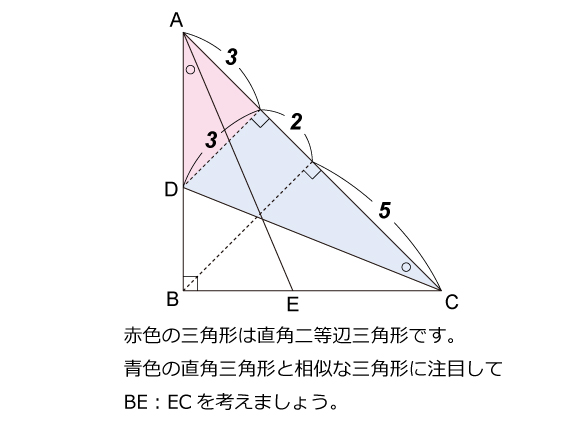



図形ドリル 第233問 直角二等辺の辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦
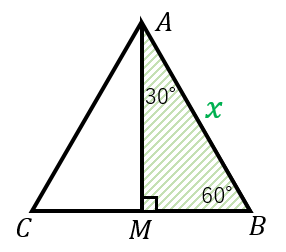



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく
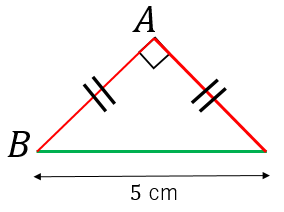



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
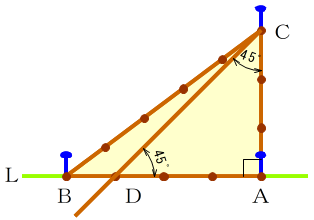



3 4 5の三角形で 本当に直角ができる Note Board




二等辺三角形の性質の証明 頂角の二等分線 Youtube




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




三角比 30 45 60 もう一度やり直しの算数 数学
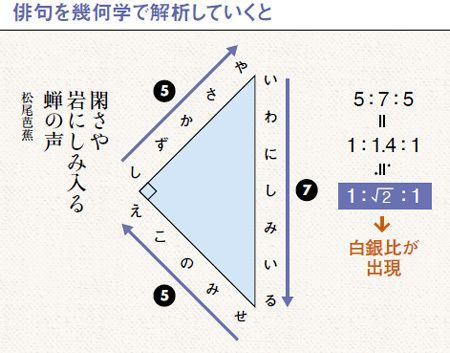



5 7 5 の俳句に隠されていた 白銀比 2ページ目 President Online プレジデントオンライン




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
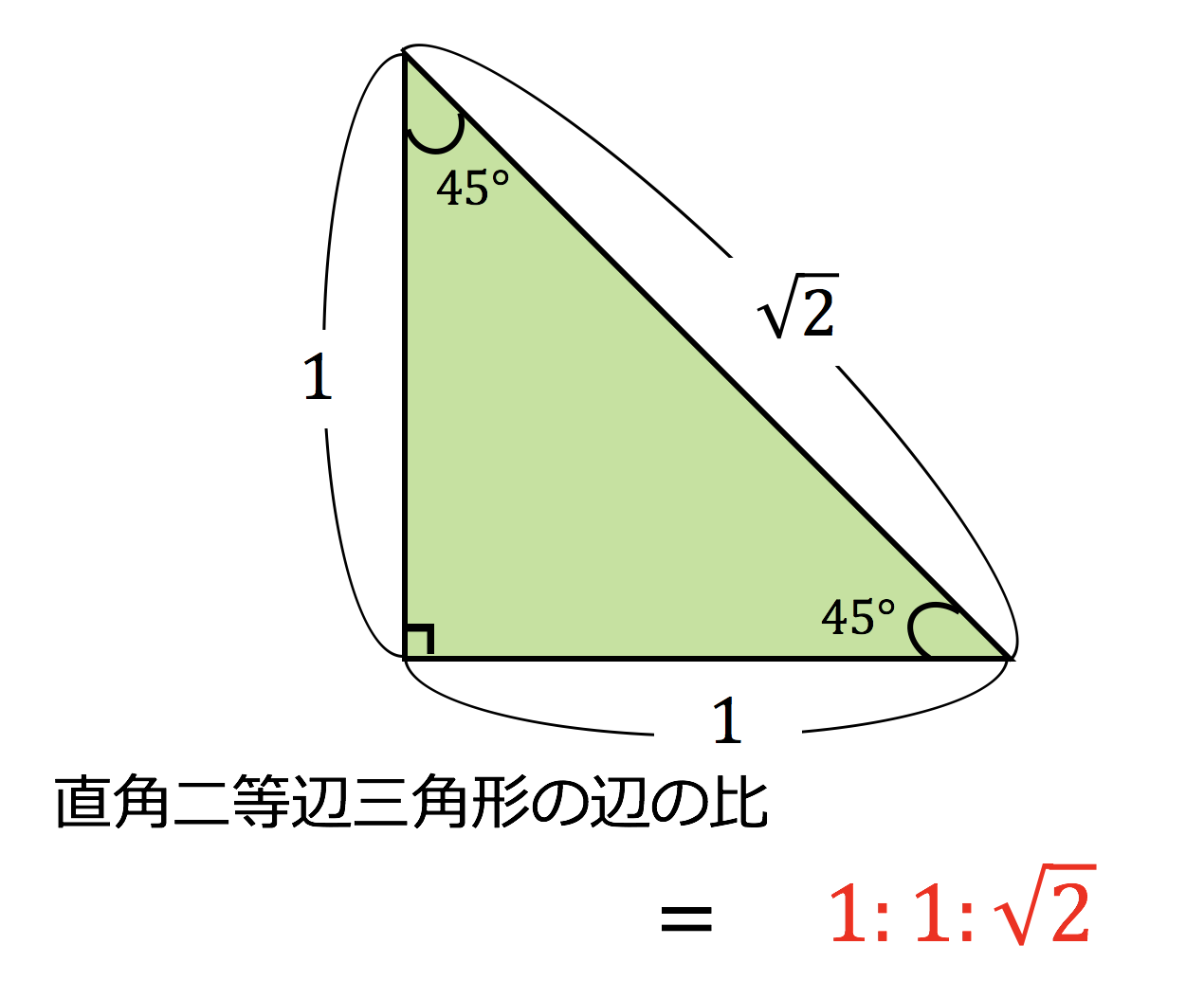



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア
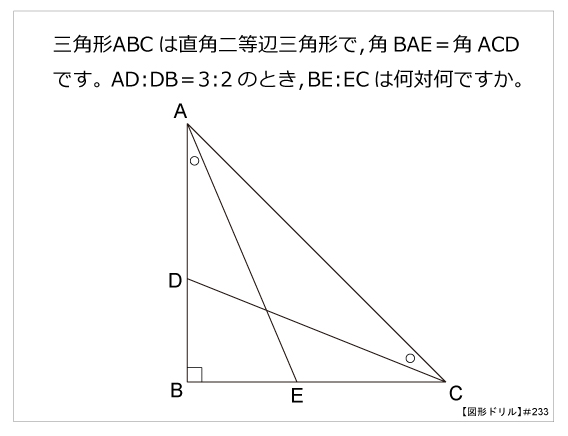



図形ドリル 第233問 直角二等辺の辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




直角三角形面積直角三角形面積公式求救 Kelp




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



この図でなぜ直角二等辺三角形三角形の比が1 1 2 となるので Yahoo 知恵袋



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



Es0sitebydfbkm




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



直角三角形の高さは 1分でわかる計算 求め方 公式 直角二等辺三角形の辺の長さ




二等辺三角形 Wikipedia




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube



高校入試 英語 数学 特別な直角三角形



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




特別な直角三角形の辺の比 無料で使える中学学習プリント
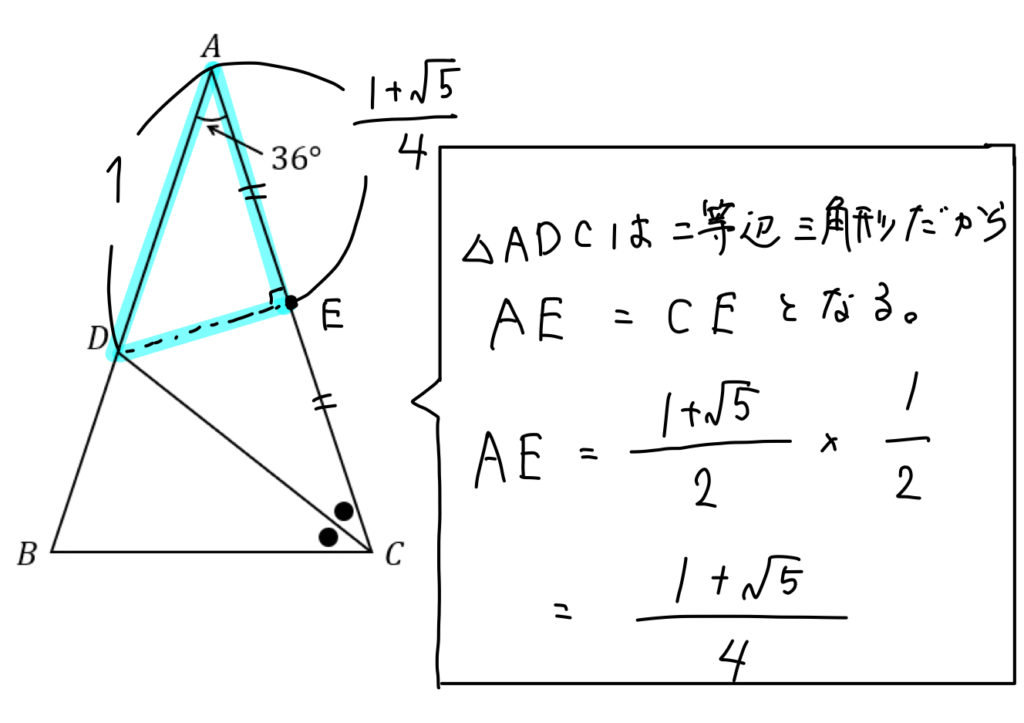



数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
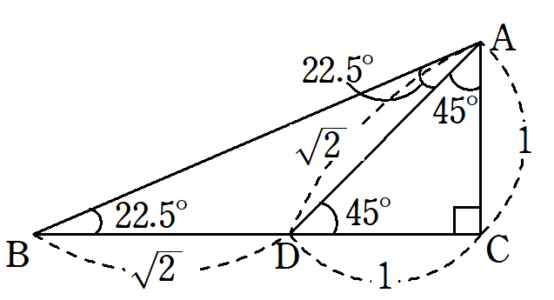



22 5 の三角比 Fukusukeの数学めも




三平方の定理と二等辺三角形 Youtube




直角二等辺三角形10枚で正方形 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




よく使う三角比の値 数学i By Okボーイ マナペディア
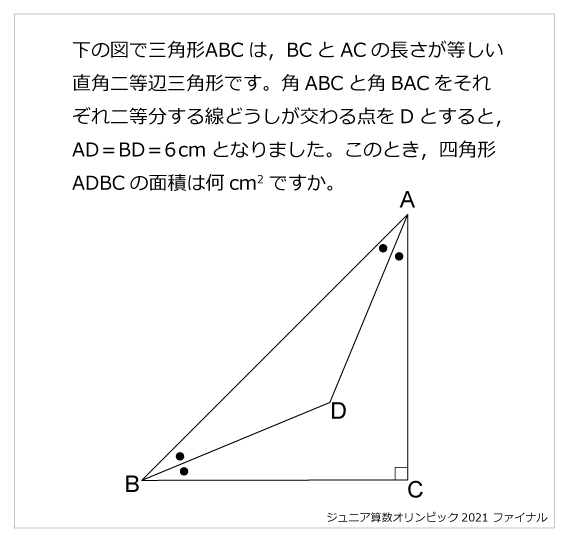



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




中学受験算数 これだけ 算数のカギ 平面図形 直角二等辺三角形 辺の長さと面積 Spi Youtube
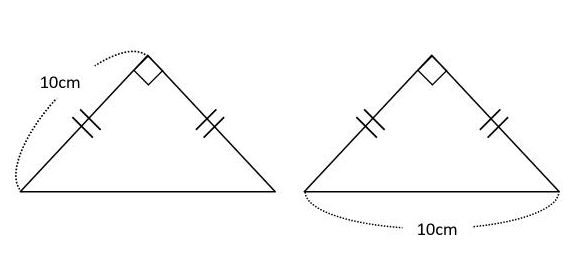



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



直角二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿