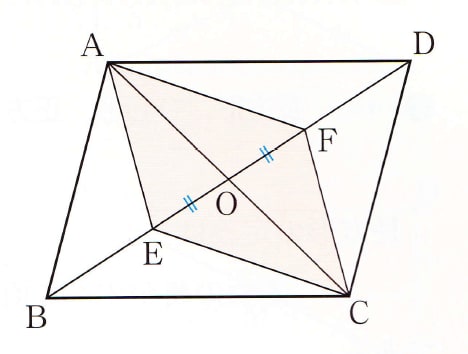
この平行四辺形になる5つの条件については、正確に暗記し、問題場面に応じて"活用できる"ことが 重要である。 2 ※図の表し方は同じ意味ならよい。 <証明> 平行四辺形の対角線はそれぞれの中点で交わるので ao=co ① bo=do ② 仮定より be=df ③ ②③より eo=bo-be=do-df=fo よって、eo=fo ④ ①④より 対角線がそれぞれの中点で交わるので 四角形aecfは平行四辺形である。・平行四辺形の性質を利用して、図形の証明をすることができる。 ・証明の結果からわかった、新たな性質を理解することができる。 (2)本時の指導について 本時の授業では、関連づけを図る(別の場面に置き換える)課題を扱い、平行四辺形の性質

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
中学2年 数学証明平行四辺形
中学2年 数学証明平行四辺形- このノートについて えびまる 平行四辺形になるための条件についてまとめました! 教科書は東京書籍です。 三角形と四角形 平行四辺形 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることができます! 中二の平行四辺形の証明です! 個人的に難しいのをピックアップしました‼️ 学年 中学全学年, キーワード 中二,数学,平行四辺形,証明,math




中2 数学 平行四辺形になるための条件 なんでこうなるのかが わかりません Clear
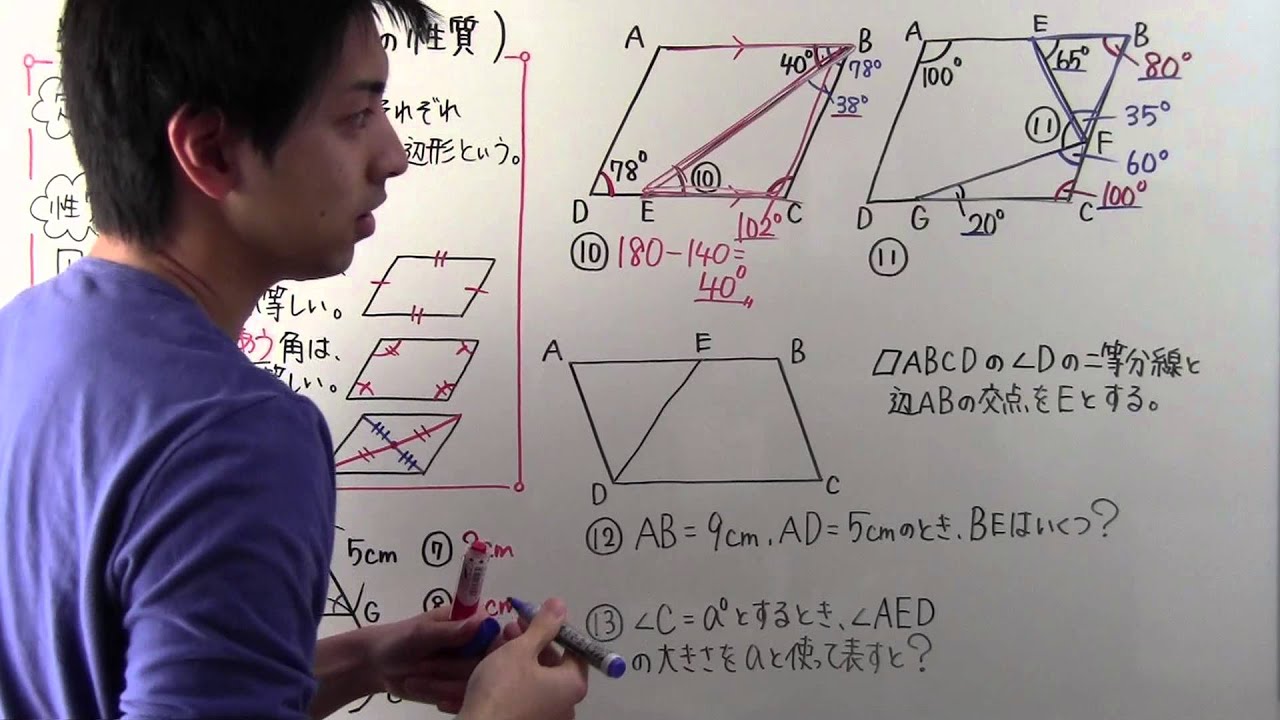
今回は、実際にある四角形が 「平行四辺形であることの証明」 をしていくよ。 ポイントは、前回学習したことと同じ。 以下の5つの条件のうち、1つでも満たせば平行四辺形であることが言えるよ。下の図は特別な平行四辺形をまとめたものです。それぞれの にあてはまる語をいれて、 文章を完成させなさい。 2 下の図は、四辺形をまとめたものです。①から⑤にあてはまる四角形の名称を答えなさい。 ① ② ③ ④ ⑤平行四辺形の性質①「平行四辺形の向かい合う辺は等しい」を証明する。 AB ∥ DC、AD ∥ BC ならば、AB=DC、AD=BCである。 このことを証明しなさい。 AB=DC、AD=BCを導くために、2つの合同な三角形を見付ける。 等しい辺や角を探し、等しい印や記号で
三角形の合同の証明の利用 四角形 \(abcd\) が平行四辺形であることを示すために、 辺の長さ、角の大きさが等しいことを示したいときがあります。 これを示すために、 「三角形の合同を証明し、そこから示す」 ということ前の時間の証明 平行四辺形の対角線は 参照 「平成30年度 報告書 中学校 数学」p121~p127, 「平成30年度 解説資料 中学校 数学」p117~p122 C B E平行四辺形の定義 ①定義 2組の対辺がそれぞれ平行である。 ②定理 2組の対辺がそれぞれ等しい。 ③定理 2組の対角がそれぞれ等しい。
平行四辺形の角度、辺の長さ まとめ お疲れ様でした! 平行四辺形の角度、辺の長さ問題では そこまで『難しい』と困ってしまうようなものはありませんね。 平行四辺形の基本性質を覚えておくだけで簡単に解けるものばかりです。 平行四辺形の基本性質2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。今回は、 「平行四辺形の特徴を使った証明問題」 を学習しよう。 前回の授業では平行四辺形の特徴を4つ覚えたよね。 POINT



数学平行四辺形の証明でアルファベットの順番 問題は次の角と等 Yahoo 知恵袋



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
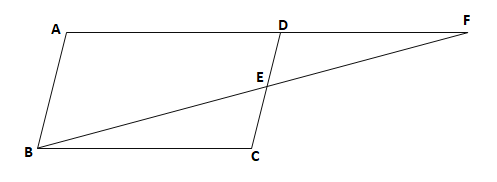
平行四辺形の性質1 a b c d 平行四辺形の定義(ab//cd, ad//cb)から、2組の対辺はそれぞれ等しい(ab=cd, ad=cb)を証明する。 平行四辺形の証明では、ほぼ100%使うと思っていていいでしょう。 次の平行四辺形に関する証明は、「 平行四辺形の性質をつかっておこなう証明 」と「 平行四辺形になることを証明 」と大きく2つあります。Abcdでde=bfのとき、四角形ebfdが平行四辺形になることを証明する。 a b c d e f 平行四辺形の対辺はそれぞれ平行なのでad//bc、よってde//bf 仮定よりde=bf 1組の対辺が平行でその長さが等しいので四角形ebfdは平行四辺形となる。 図形の証明の方法は1通りとは限らない。




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方



1
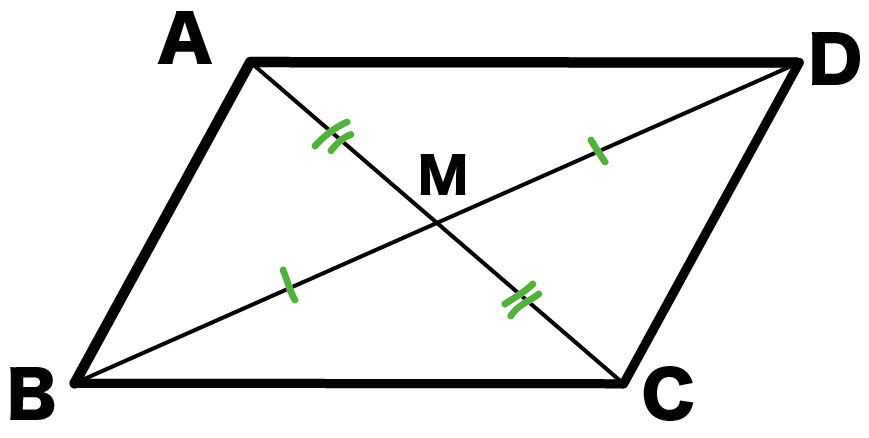
課題学習の指導(数学) 1.指導のねらい (1) 「平行四辺形になるための条件」の理解の深化を図る。 (2) 補助線の引き方を学ぶ。 〈課題学習〉 (3) 補助線を引くことで,図形の重要事項を復習し,その定着を図る。 〈課題学習〉 2.指導計画四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。 ( 定義 ) 2 2組の向かいあう辺が、それぞれ等しい。 ( 証明 ) 3 2組の向かいあう角が、それぞれ等しい。 ( 証明 ) 4 対角線が、それぞれの中点で交わる。 ( 証明 )2 2組の向かいあう辺が、それぞれ等しい。 abcと cdaで、 ab=cd 1 bc=da 2 ac=ca(共通) 3 1,2,3より3辺がそれぞれ等しいので、




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
平行四辺形3 abcdの対角線bd上に頂点aとcから垂線を下ろしその交点をe,fとする。 a b c d e f abe≡ cdfを証明せよ。 (1)の結果を 平行四辺形になる条件は、言葉だけでなく図形とセットで覚えるのがポイントです。 では、以上のことを踏まえて次の問題を解いてみましょう。 問題:次の (1)~ (4)のうち、平行四辺形であるといえるものを選びなさい。 よし。 ひとつずつ図形を書いて 中2数学の平行四辺形の証明についてです!! もう直ぐ冬休みです* 明日まで頑張ります(´ω`) 学年 中学2年生, 教科書 未来へひろがる数学2 啓林館, 単元 証明, キーワード 中2,数学,証明,平行四辺形,math




数学 中2 74 平行四辺形になる条件 Youtube



平行四辺形の性質1
⑧、⑨より1組の対辺が平行でその長さが等しいので四角形ebgdは平行四辺形となる。 よってbe//dg・・・⑩ ④よりfg//he ⑩よりef//gh よって2組の対辺がそれぞれ平行なので四角形fgheは平行四辺形となる。 四角形amcdにおいて an=cn(nはacの中点) mn=nd(仮定) 1平行四辺形の性質 2平行四辺形になる条件 3特別な平行四辺形(長方形・ひし形・正方形) 4平行線と面積 等積変形 学年平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件 があります。



中2数学 発展問題プリント12 平行四辺形3 長方形とひし形 問題 232



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ
中学数学平行四辺形の証明問題を徹底解説! kaztastudy 今回は、中2で学習する証明問題の単元から 平行四辺形の証明問題について取り上げていくよ!平行四辺形の特徴は、 ① 「2組の対辺(向かい合う辺)が、それぞれ平行」 に加えて、残り3つ。 キーワードは、 「辺」 、 「角」 、 「対角線」 だよ。 まずは、 「辺」 から。 ② 「2組の対辺がそれぞれ等しい」 向かい合う辺の長さ が、それぞれ等しいんだね。 次に、 「角」 。 ③ 「2組の対角がそれぞれ等しい」定義は「こういう四角形を平行四辺形としよう」と決めたことなので、これを証明することはできません。 「なぜ平行四辺形の向かい合う2組の辺は平行なのか?」と問われたら、 「そのような四角形が平行四辺形と定義されているから」 という答えになってしまいます。




中2数学 平行四辺形の証明 例題編 映像授業のtry It トライイット



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同
平行四辺形の性質を利用した証明 次の証明をしなさい。 abcdの対角線bdに頂点a,cからそれぞれ垂線を下ろしその交点をe,fとする。このときbe=dfとなることを証明せよ。 a b c d e f abcdでbe=dfである。このときae=cfとなることを証明せよ。 a b c d e f abcdの対角線の交点をoとする。 三角形の内角の和が180°であること、直線が180°であることを利用します。 平行四辺形(1) 平行四辺形と直角三角形のパターンです。 直角三角形の合同と錯角を利用します。 平行四辺形(2) 平行四辺形を対角線を利用して証明するパターン。 ある四角形が平行四辺形になることを証明する問題をどういう風に考えて解けばいいかが分かります。 ⭐️無料で読めるClearの「塾ノート」⭐️ ・塾の先生が教科のポイントや勉強法をまとめています ・自主学習・定期テスト対策・受験勉強に役立ちます ・自分に合った塾を選ぶ参考に




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット




平行四辺形になることの証明 Youtube
平行四辺形になるための条件 四角形 \(abcd\) が平行四辺形であることを示せ。 このような問題を学習していきます。 四角形 \(abcd\) が平行四辺形であることを示すためには、 以下の \(5\) つのうち、ど な問題が,21の都立西にあったのでご紹介します。 問1,問2中2の図形証明分野習った後に解ける 問3相似習った後に解ける 芸術的な難問高校入試 第52回 「平行四辺形の超難しい証明」 出典:令和3年度 都立西高校(独自作成校) 過去問 数学 範囲数学25章図形の性質と証明「平行四辺形の性質」<応用問題・解答> 1 (証明)平行四辺形の性質より AD// BC・・・① F AD=BC・・・② また,仮定よりBE=DF・・・③ ②,③より AF=EC・・・・④ また,①よりAF// EC・・・・⑤




ベクトルの外積と平行四辺形の面積 身勝手な主張



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd
(1) 平行四辺形の向かい合う辺は等しいので,ad=bc (2) 平行四辺形の向かい合う角は等しいので,∠D=∠B (3) ∠B+∠C=180°なので,∠C=180°-∠B=180°-75°=105°平行四辺形になるための条件 四角形 \ (abcd\) が平行四辺形であることを示せ このような問題を学習していきます 四角形 ある四角形が平行四辺形となるための条件について解説します 丸暗記ではなく、なぜこの条件が1つでも成り立てば平行四辺形と言えるのか?




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室



平行四辺形の性質 中学2年 数学クラブ




中2の数学の問題です 平行四辺形になるための条件の部分で 対角線がそれぞれ中点で交わ Clear




Math 平行四辺形 平行四辺形になることの証明 働きアリ



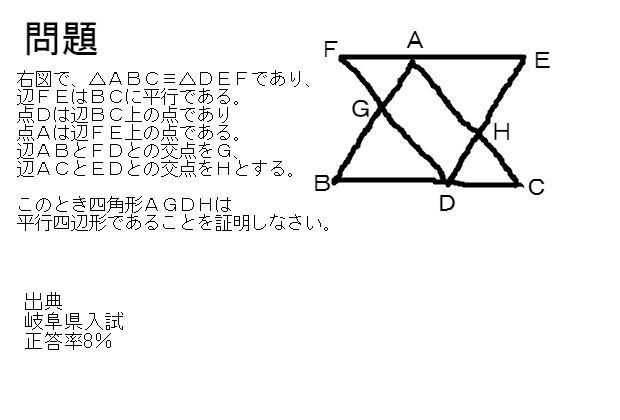
証明 は と が Takapの数学日記



平行四辺形になるための証明1



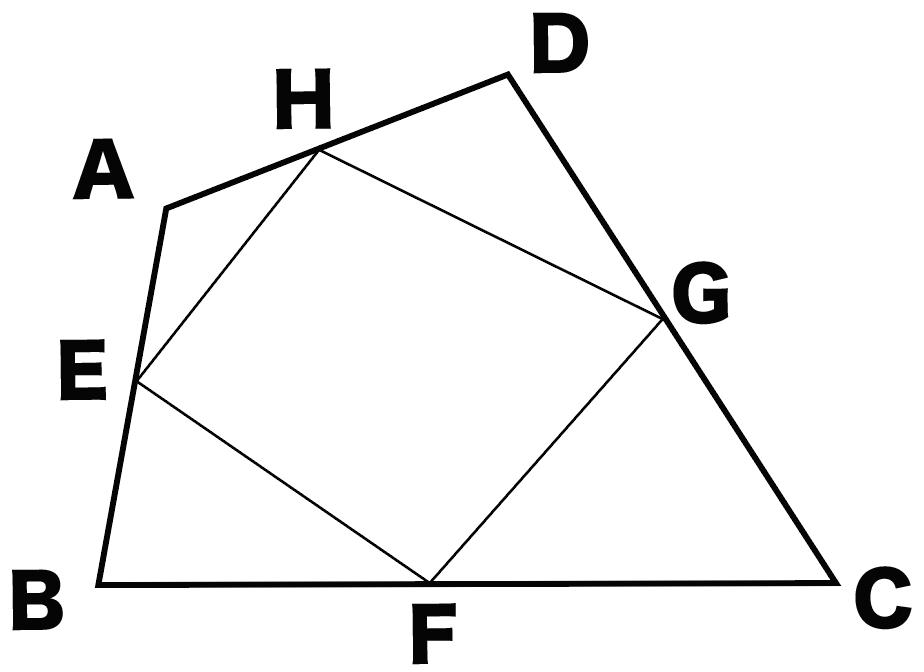
正答率8 の証明問題 平行四辺形 中学数学 理科 寺子屋塾の復習サイト
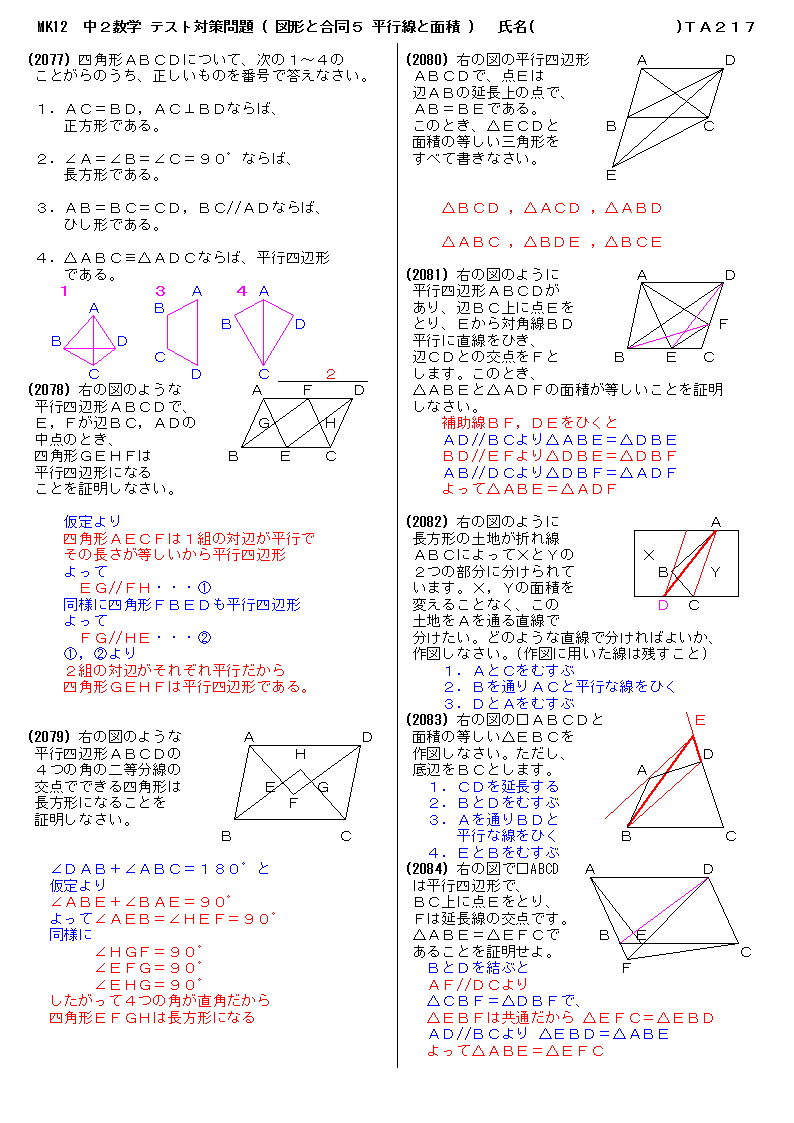



無料 中2数学 テスト対策 解答プリント 217 図形と合同5 平行線と面積



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧



至急 数学証明平行四辺形の折り目の問題です どなたかご教示お願い致し Yahoo 知恵袋




無料 中2数学 標準問題 解答プリント 230 平行四辺形1 性質




中学2数学 20 特別な平行四辺形の証明 2 Youtube




高校数学b ベクトルの成分表示と平行四辺形 受験の月



19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
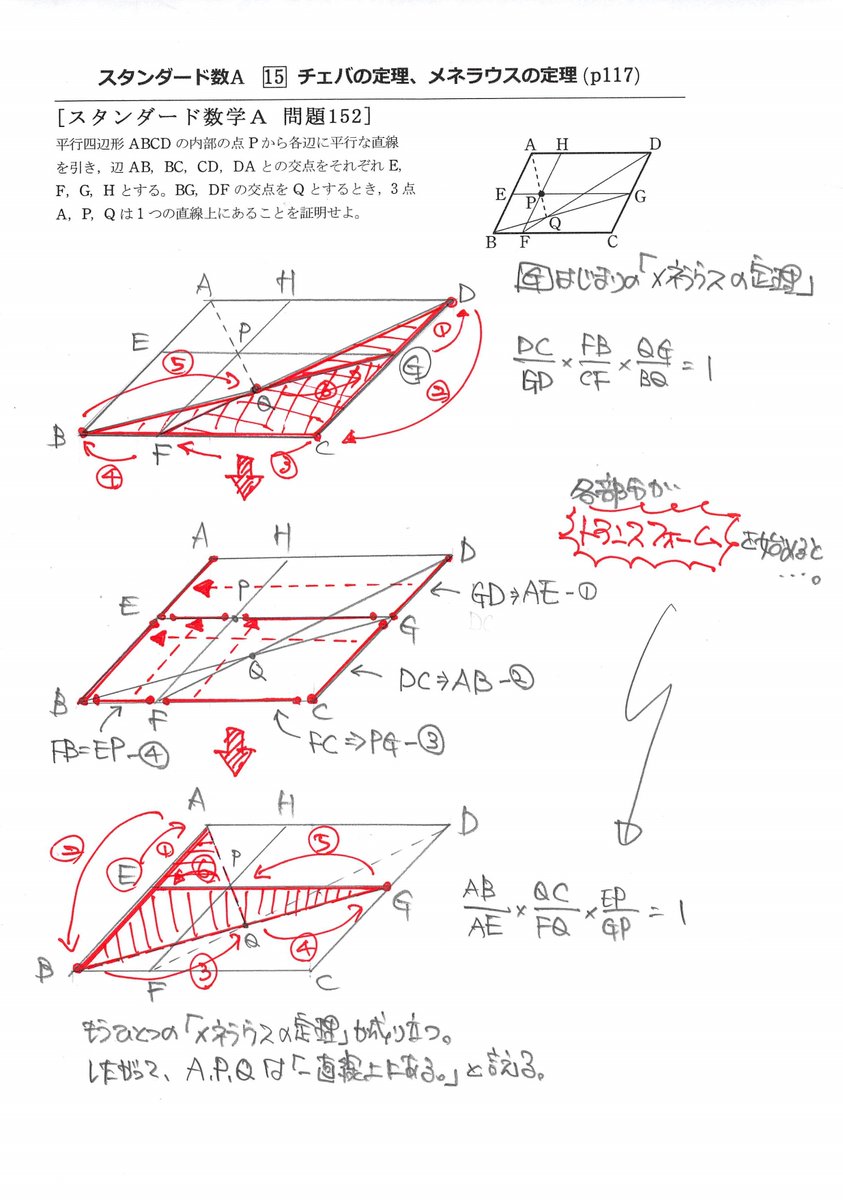



Twitter पर S Live数学館 数研スタンダード数a 2章 図形の性質 15チェバの定理 メネラウスの定理 問題152 P117 出題者は きっとsf好きに違いないですね 何しろ 平行四辺形が トランスフォーム して 新たな平行四辺形ができるのですから Sf
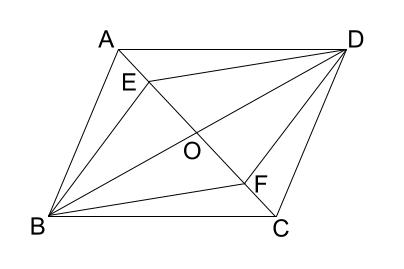



中学数学 平行四辺形になることの証明 その1 中学数学の無料オンライン学習サイトchu Su




四角形 Ict教材eboard イーボード




平行四辺形の証明問題 無料で使える中学学習プリント




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




中2 数学 平行四辺形になるための条件 なんでこうなるのかが わかりません Clear
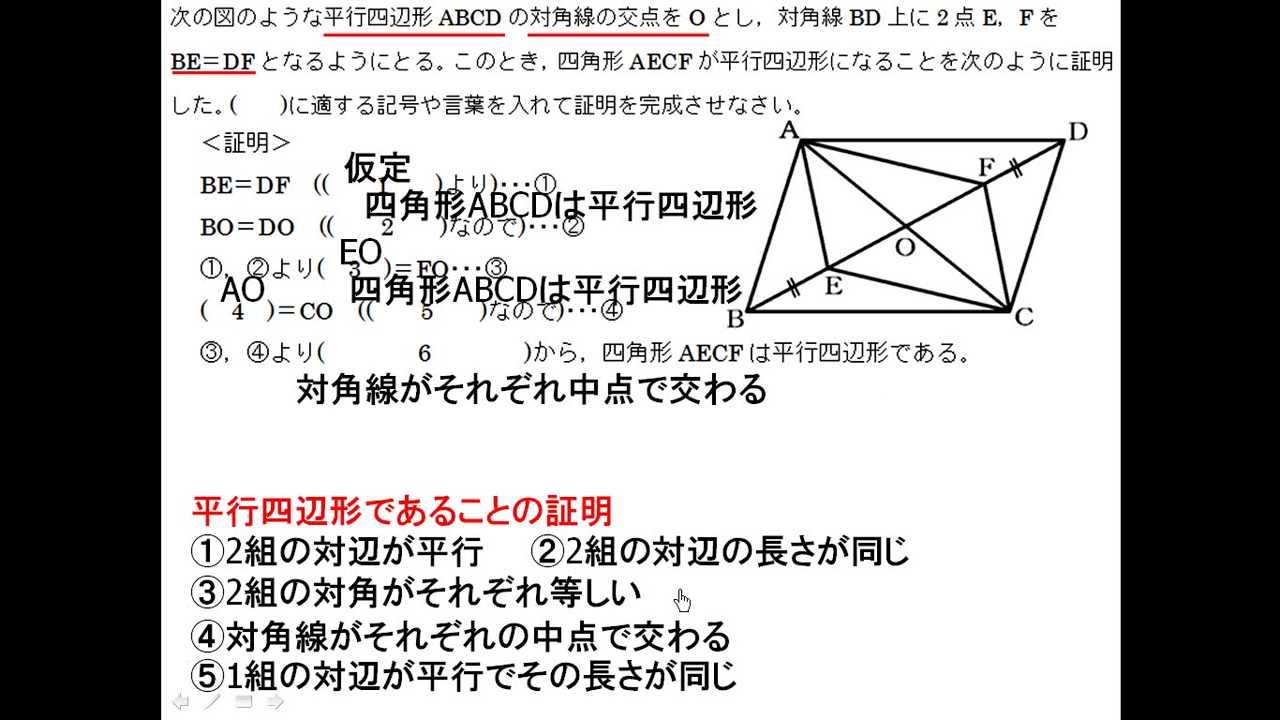



中2 数学 5 3 平行四辺形の証明 Youtube
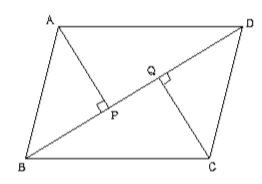



中2数学 平行四辺形の証明のポイントと練習問題 Examee




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




平行四辺形と証明 Youtube



平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン




中2数学 平行四辺形の証明の定期テスト予想問題 Pikuu
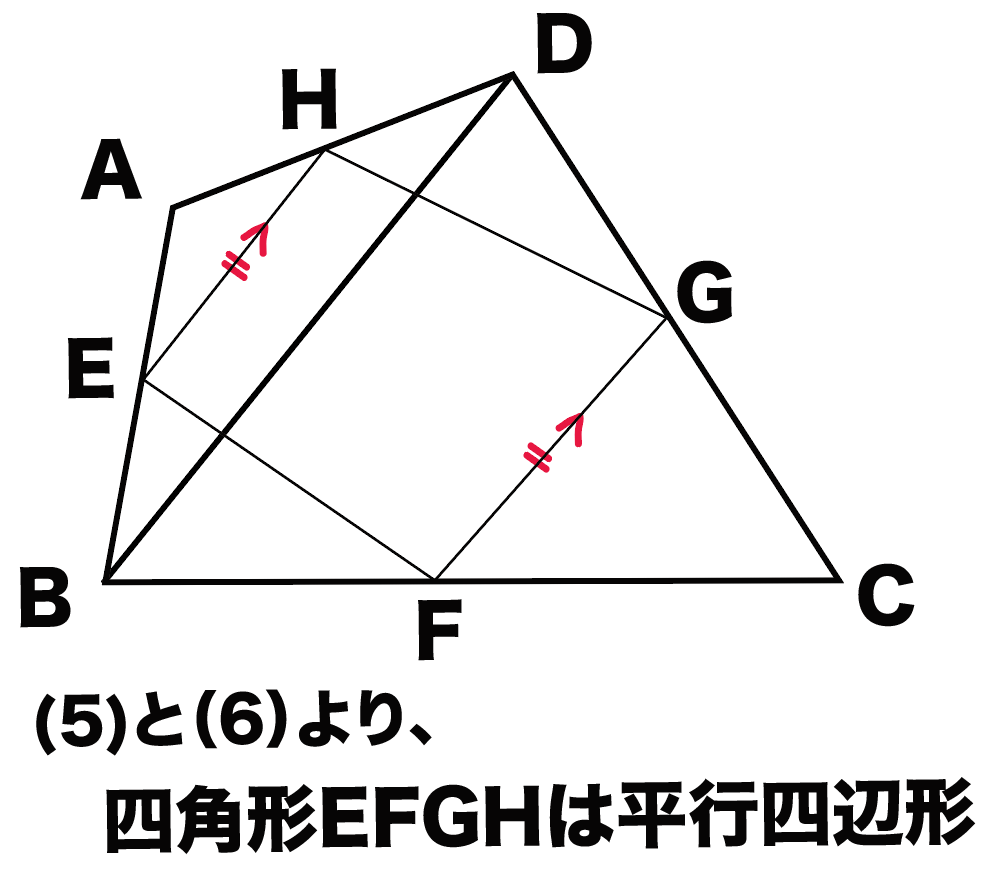



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形 中学数学で遊ぶ 身勝手な主張



1



中2数学 基本問題プリント12 平行四辺形1 性質 問題 230



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧



数学 中2 73 平行四辺形の性質 Youtube




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




中2 数学 平行四辺形になるための条件 中学生 数学のノート Clear




中2 数学 証明 この平行四辺形の証明を教えて下さい 画像悪くてすみ Okwave




中学数学 平行四辺形の証明問題が誰でもできるようになる方法 平行四辺形と辺を共有しない問題 中2数学 Youtube



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




この証明の問題の 4 がわかりません Clear




1 2 5 2 Descubre Como Resolverlo En Qanda



中2数学 平行四辺形の性質と証明の要点まとめノート 中学生勉強サイトあかね先生
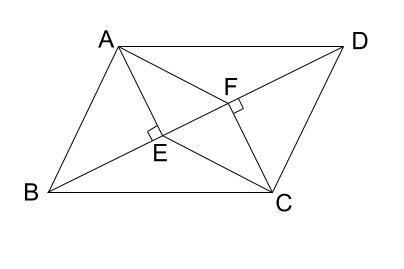



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




中2 数学 中2 証明 中学生 数学のノート Clear
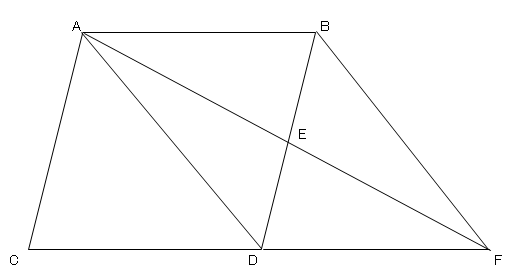



平行四辺形の証明 2 ネット塾




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
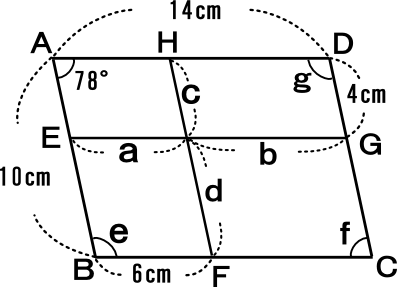



中学2年数学練習問題 図形と合同 平行四辺形の性質と証明問題
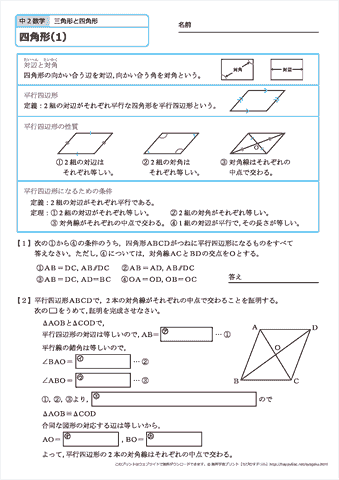



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Wordで使える平行四辺形 2 Wordで数学問題プリントを作ろう
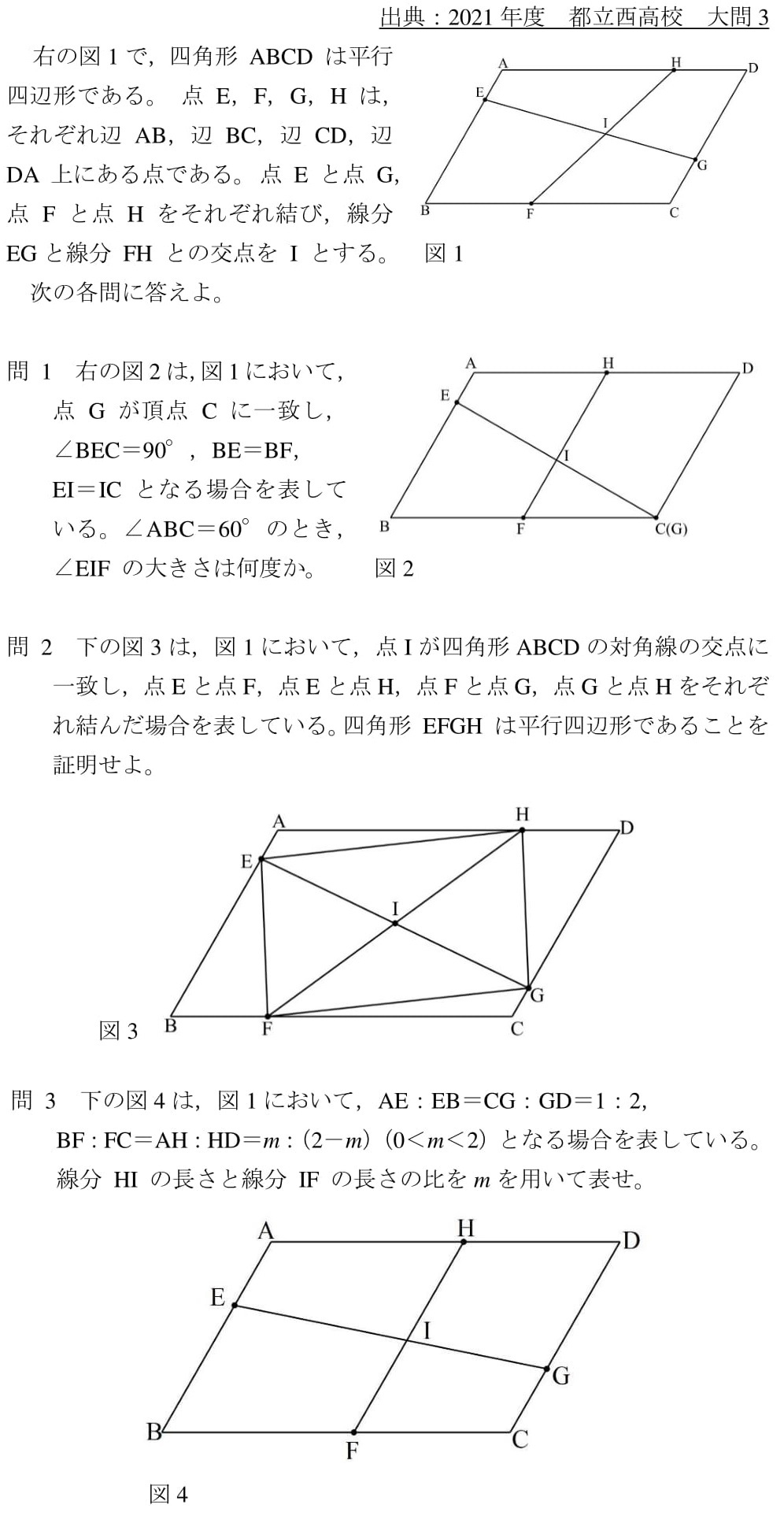



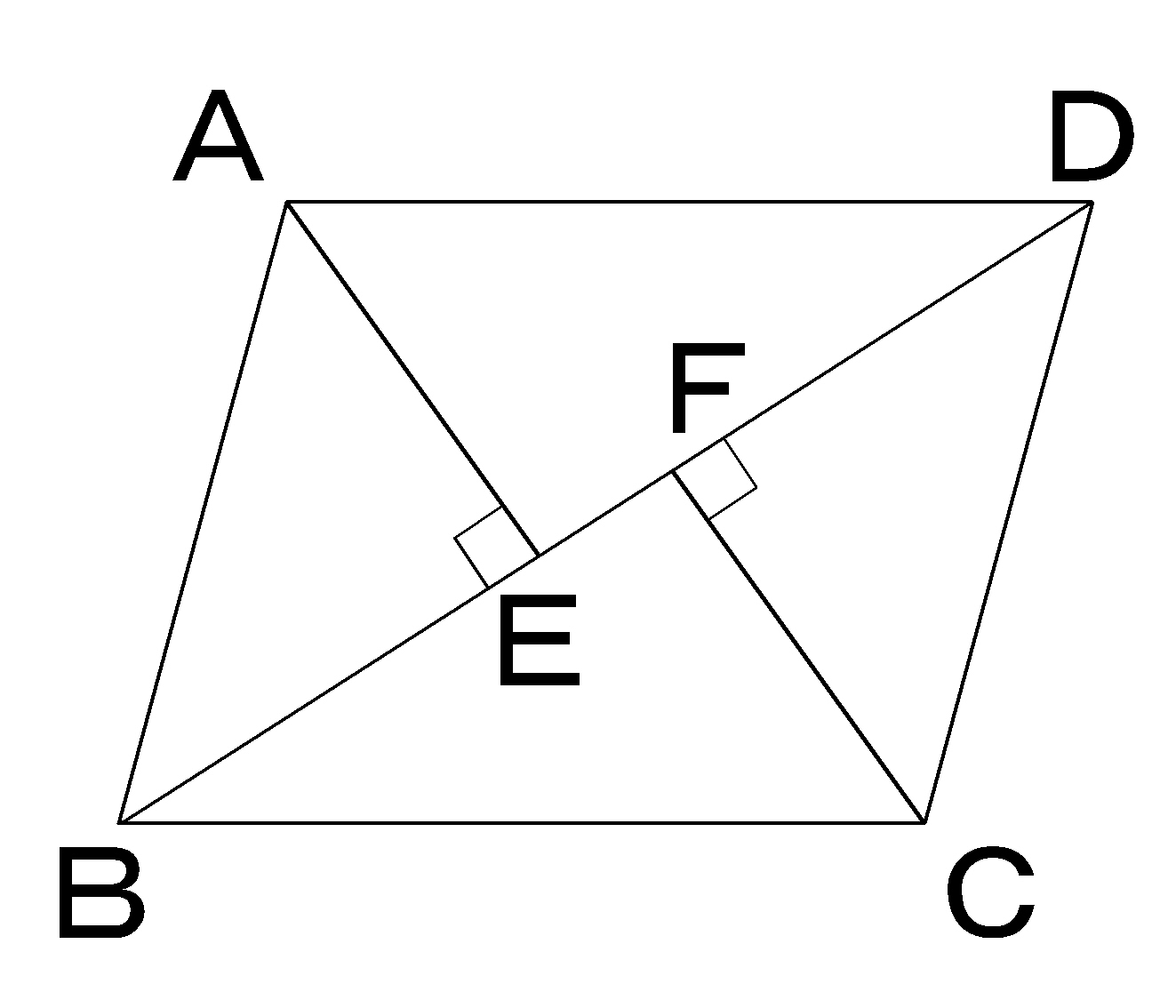
21都立西 平行四辺形の難問証明 高校入試 数学 良問 難問




中2 中2数学 平行四辺形の証明 授業ノート 中学生 数学のノート Clear
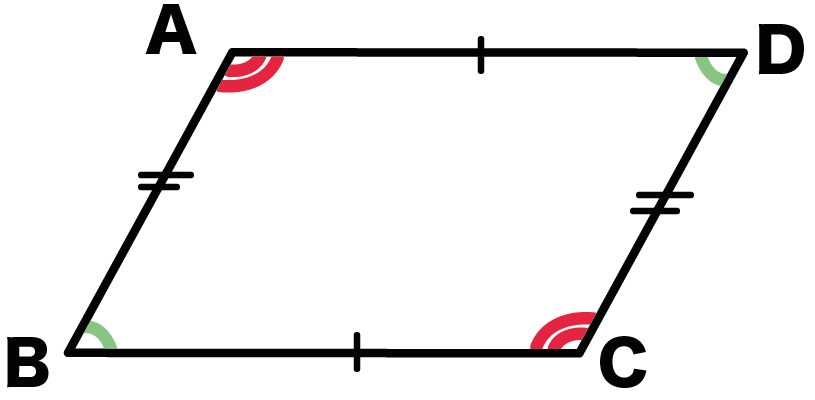



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




証明が全く分かりません汗 教えてください Clear




世界一わかりやすい数学問題集中2 5章 図形の性質と証明
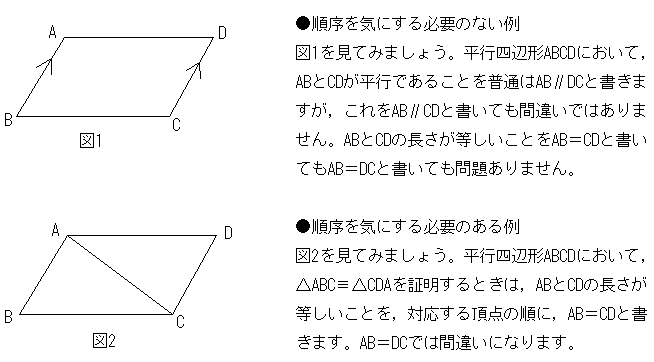



三角形と四角形 平行四辺形の辺や角の表記の順序 中学数学 定期テスト対策サイト




中2 数学 四角形3 平行四辺形の証明1 11分 Youtube




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




平行四辺形を使った証明 Youtube




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
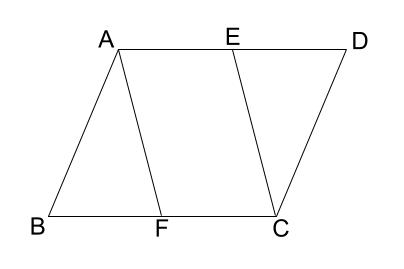



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
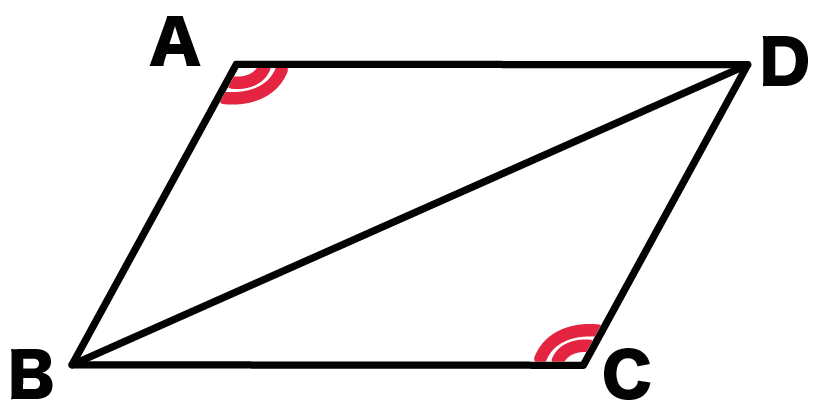



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形



1




無料 中2数学 標準問題 解答プリント 231 平行四辺形2 条件と利用




平行四辺形の定義と性質 証明問題の解き方 数学fun




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




中学校数学 証明のコツ 年01月




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




中学校数学 証明のコツ 平行四辺形と錯角 同位角の相互関係を理解する過程で 証明する力を確実に伸ばすことができる自学自習教材




中2数学 合同証明 平行四辺形であることを証明 Youtube




中二 数学 証明について この画像の問題についてで 上が問題下が答えなん Okwave




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




無料 中2数学 標準問題 解答プリント 232 平行四辺形3 長方形とひし形




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear



中2数学 標準問題プリント12 平行四辺形1 性質 問題 230




中2 中2数学 平行四辺形 中学生 数学のノート Clear




中2数学 平行四辺形の性質の利用 例題編 映像授業のtry It トライイット
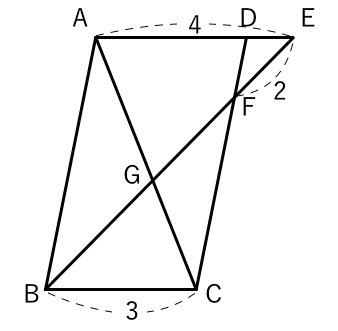



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
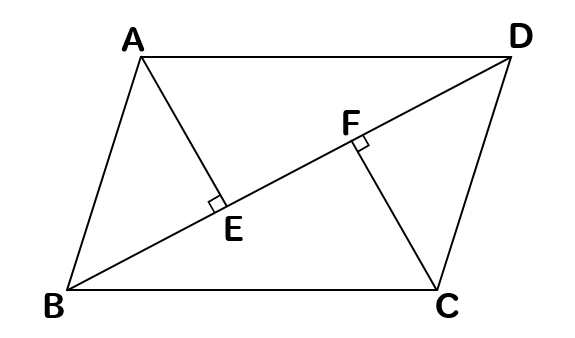



中学数学 平行四辺形の証明問題を徹底解説 数スタ
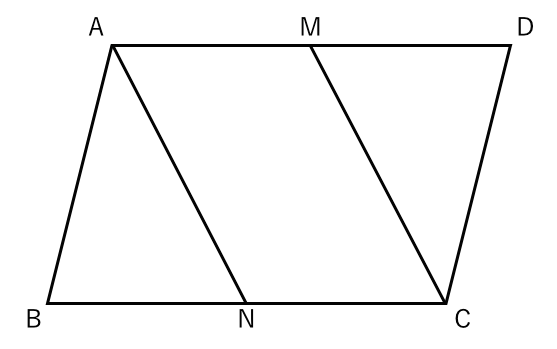



平行四辺形であることを証明する 苦手な数学を簡単に
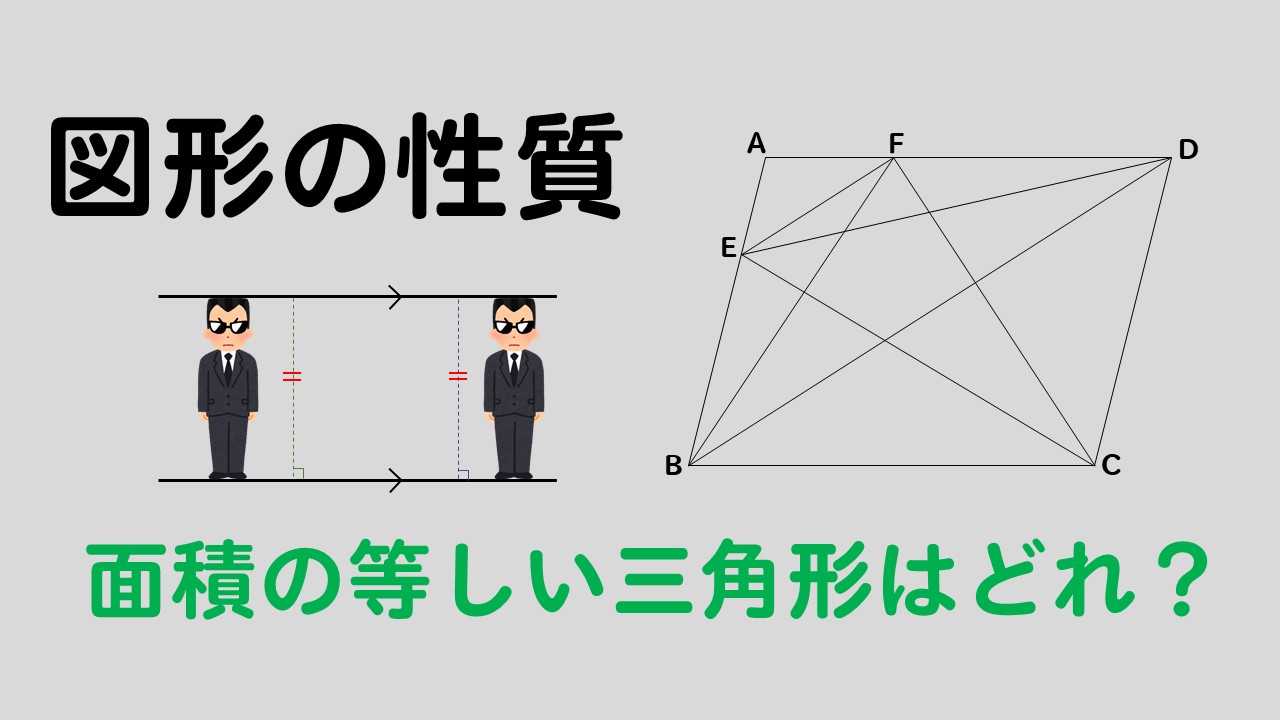



中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1




平行四辺形になることの証明 Youtube




中学数学 平行四辺形になることの証明 その3 中学数学の無料オンライン学習サイトchu Su
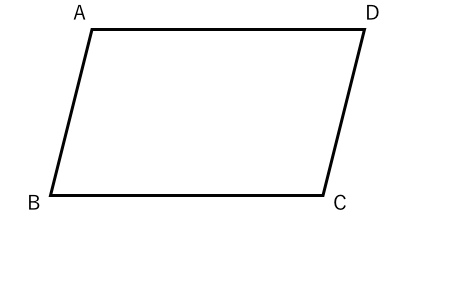



合同な三角形 平行四辺形で証明 苦手な数学を簡単に



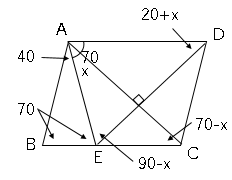
数学の証明の問題です 平行四辺形abcdの外側に 辺ab をそれ Yahoo 知恵袋



0 件のコメント:
コメントを投稿