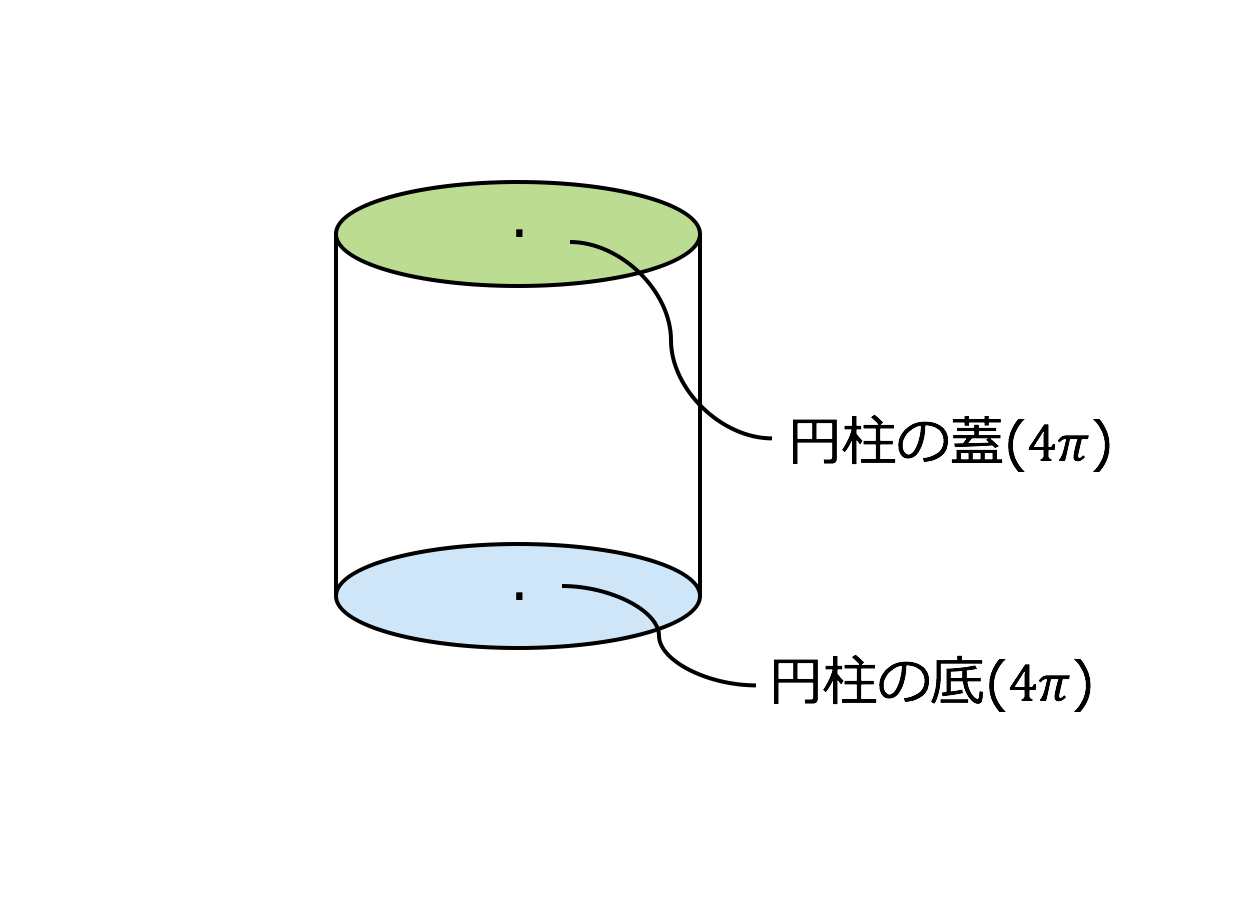
円柱の体積 $v$ は、 円周率× 半径 × 半径 × 高さ 円柱の表面積 $s$ は $2$×円周率× 半径 × 半径 +$2$×円周率× 半径 × 高さ円柱の表面積を求めるには、まず上下の円の部分と側面の部分を分けて考えます。 側面部分は筒状ですが、開いて四角形の状態にします。 円の面積は 半径×半径×円周率 なので、上下の円の面積を求めY) (2) S 円柱面x2 y2 = R2;
1
円柱 の 面積 計算
円柱 の 面積 計算- よって、円柱の表面積は\(168\pi (cm^2)\)となります。 円柱の表面積を求める公式 $$(底面積)\times 2(側面積)$$ 円柱の体積を求める方法 円柱の面積分についての問題です。 円柱Vの表面積をSとし、その単位法線ベクトルをnとするときの面積分∬(s)a・ndsを求めなさい a = x^2i xyj z^2k V x^2 y^2 = 1, 0 ≦ z ≦ 1 出来れば途中計算も含めて教えていただけたら助かります。




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
0 ≦ z ≦ h, で円柱の側面の正の単 位法線ベクトルは内部から外部に向かってひくものとする小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S
よって、断面積は、 4(1-k 2 ) となる。 これを、 k=-1~1で積分して体積が得られる。 すなわち、 2 3つの円柱の場合 円柱の中心軸を x、y、z とし、原点で直交しているものとする。このときでき2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。
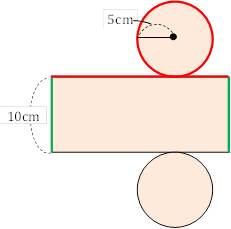
まずは、円柱の体積を求めよう! というわけで、まずは円柱の体積を求めます。 底面積 8\times 8\times 314=096 (cm^2) 円柱の体積 096\times 10=096 (cm^3) かず先生 体積を求めたら、それをリットルに変換します!円柱の表面積を求める公式は、次の通りです。 S = 2πr2 2πrh = 2πr(r h) S = 2 π r 2 2 π r h = 2 π r (r h) ここで、S は円柱の表面積、π は円周率、r は底面の円の半径、h は高さを表します。(球の表面積が、球に外接する円柱の側面積に等しいことが言えればよい。) それに対して、体積の方は、 カヴァリエリ(Cavalieri)の原理 2つの立体を、平行な平面で切ったときの切り口の面積がいつも等しければ、2つの立 体の体積は等しい。
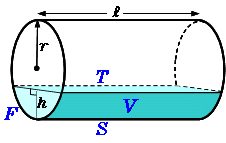



一部が欠けた直円柱の体積 高精度計算サイト
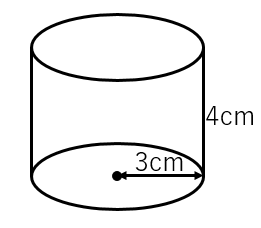



円柱の表面積と体積を求める公式 具体例で学ぶ数学
中学数学 図形 円柱とは? 体積・表面積の公式や求め方、単位あり計算問題 21年2月19日 この記事では、「円柱」の公式(体積・表面積)や実際の求め方をできるだけわかりやすく解説していきます。 また、リットルなどの単位を含む計算問題なども触した面積に作用していることになります。しかし、 接触楕円というのは、1平方ミリとか、たいていの場 合はとても小さいのです。そんな小さい面積で大き い力を受けるということになります。 このように、局所的に大きな力を受けることになる円柱の体積を求める公式は 半径×半径×円周率×高さ です。 円の面積が 半径×半径×円周率 なので、 円の面積×高さ とも言えます。



円柱の側面積の求め方を教えてください 円周 高さ円の直径 Yahoo 知恵袋
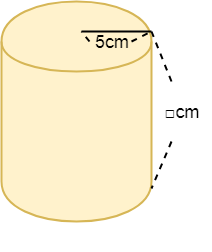



円柱の体積の求め方 公式 小学生 中学生の勉強
次の法線面積分 ∫∫ S andSを求めよ (1) S 平面x2y 2z = 2が3つの平面x = 0;y = 0;z = 0で切 り取られる部分で原点のある側を負側とする a = (2z;x;円柱の表面積 ⇒ 2πrh2πr^2 円柱の表面積は、円柱を展開したときの底面積、側面積の合計です。円柱を展開すると「円が2つ」あります。よって底面積は2倍してください。円柱の表面積の求め方は下記が参考になります。 円柱の表面積は?それは,円柱の側面積の半分と考えてよい。つまり長方形の面積の半分と考えればよく, (底辺×高さの半分,底辺はつまり円周のこと) である。 ここでようやく,西元先生の「点対称なグラフの面積は,全体の半分」の意味が読み取れることになる。




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
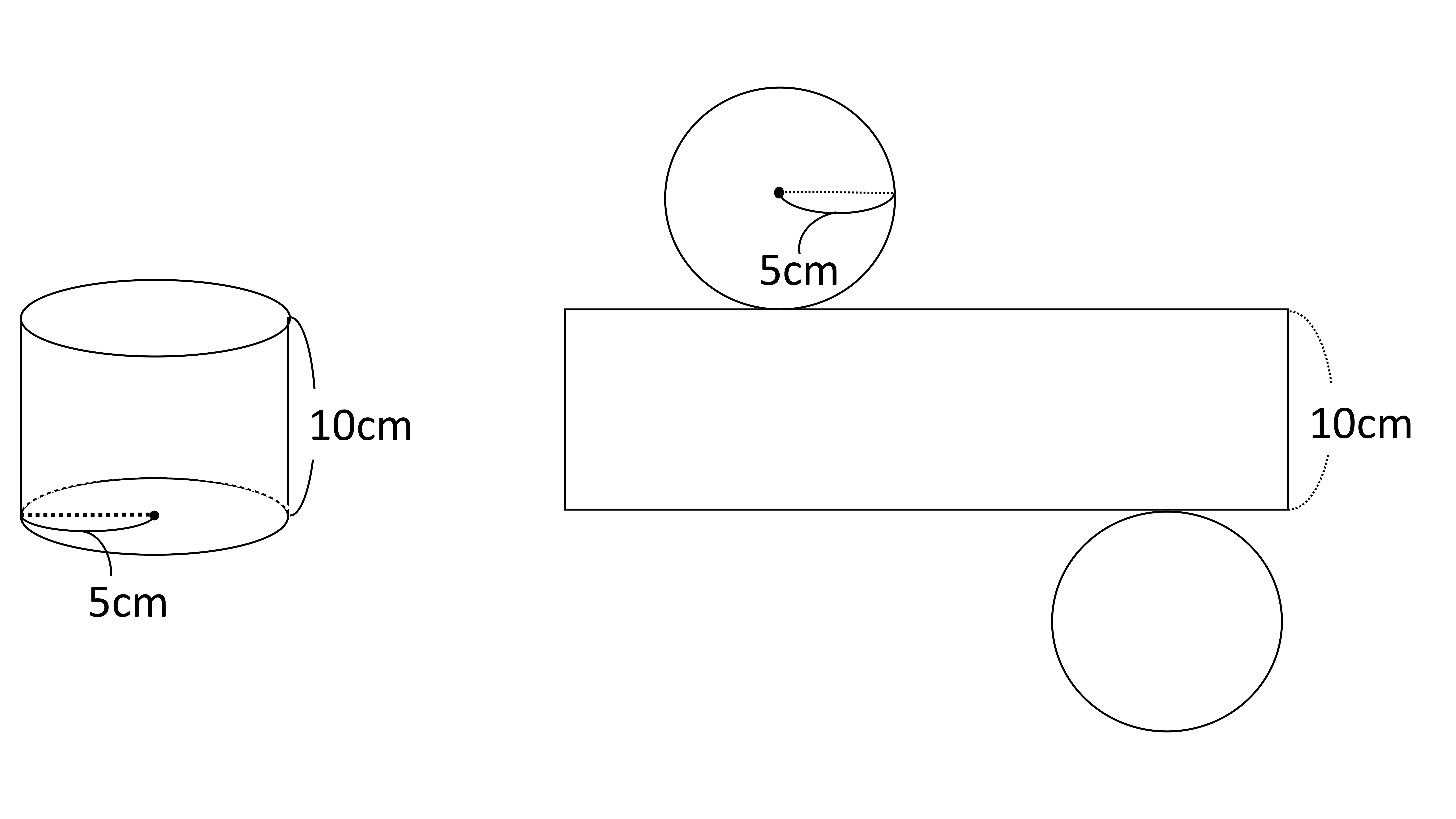
円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さから) 円柱の体積=7×7×314×12=(cm³)となります。 答え 円柱ができる。 体積はcm³ ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方公式 円柱の表面積の求め方公式 三角柱の体積の求め方公式 円錐の体積 円柱の表面積を3秒ぐらいで計算したい。 そんなときは、円柱の表面積の求め方の公式をつかってしまえば2秒ぐらいで計算できちゃうんだ。 下の図のように、円柱底面の半径をr、高さをhとすると、2πr(hr)で求めることができるよ^^ つまり、2×円周率×半径×




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円筒の面積の求め方は 1分でわかる計算方法 公式 円の面積との違い 関係
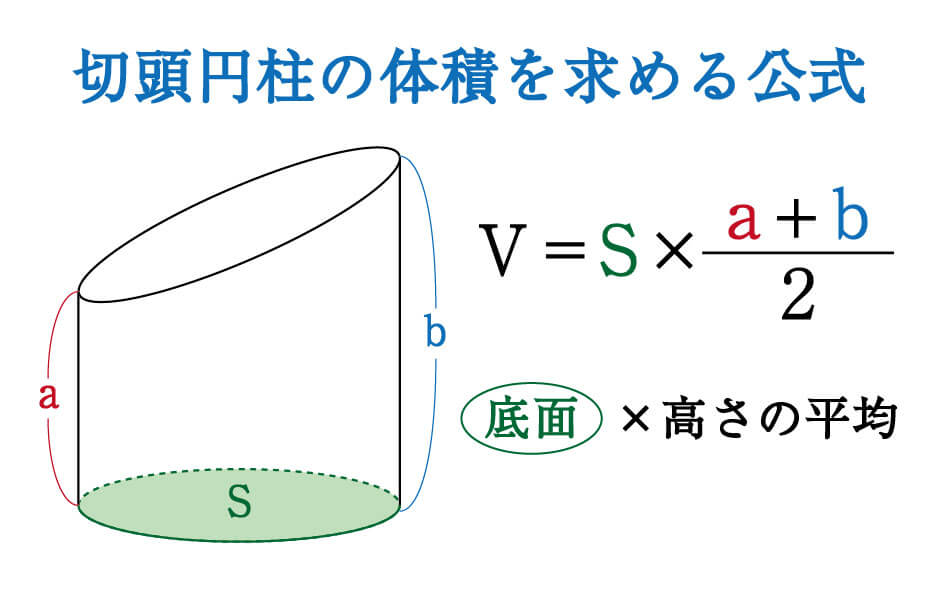
中空円の面積の求め方はS=π÷4((外円の直径×外円の直径)(内円の直径×内円の直径))だと思うのですが、中空円柱では÷4が無いのはなぜでしょうか? keisanより 円の直径 = 2 * 円の半径 より、 円の直径 2 = 4 * 円の半径 2 となるからだと考えられます。このときの円柱の高さを、h(=AC)とすると、円柱の体積は、 πb 2 h である。 AB=2a とすれば、切り口は、長径が2a、短径が2b の楕 円を表す。その面積を、S とおく。底面積=1つの底面の面積 側面積= 側面の面積の総和 だから,円柱,角柱の表面積=底面積×2側面積 となります。 また,「底面積を求めよ」というときは,1つの底面の面積を答えます。




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



1
円柱の公式(計算式) 円柱の体積V V = π r 2 h 円柱の表面積S S = 2 π r r h 円柱の側面積F F = 2 π r h微小面積要素の計算関連ページ dvの計算法 慣性モーメントとは、簡単に説明すれば物体(剛体)の回転のしづらさ、回りだす変化のしにくさを示す物体の物理的な特性のことだと考えることができるでしょう。 またさらに別の言い方をすれば回転の方程2つの直交している円柱 z2x2(a2 ① z2y2(a2 ② がある。 (1) 円柱①,②の共通部分の xy 平面に平行な平面z=tによる切り口は どのような図形か。また、切り口の面積を t の関数として表せ。 (2) 円柱①、②の共通部分の体積 Vを求めよ。




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく



1
円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付き




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ
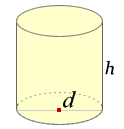



みんなの知識 ちょっと便利帳 直円柱の側面積を直径から計算する




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係
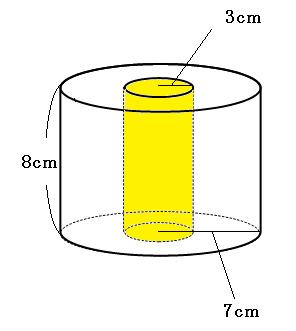



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




2 を途中式を含めて教えてください Clear




円柱の体積の求め方 公式 小学生 中学生の勉強




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
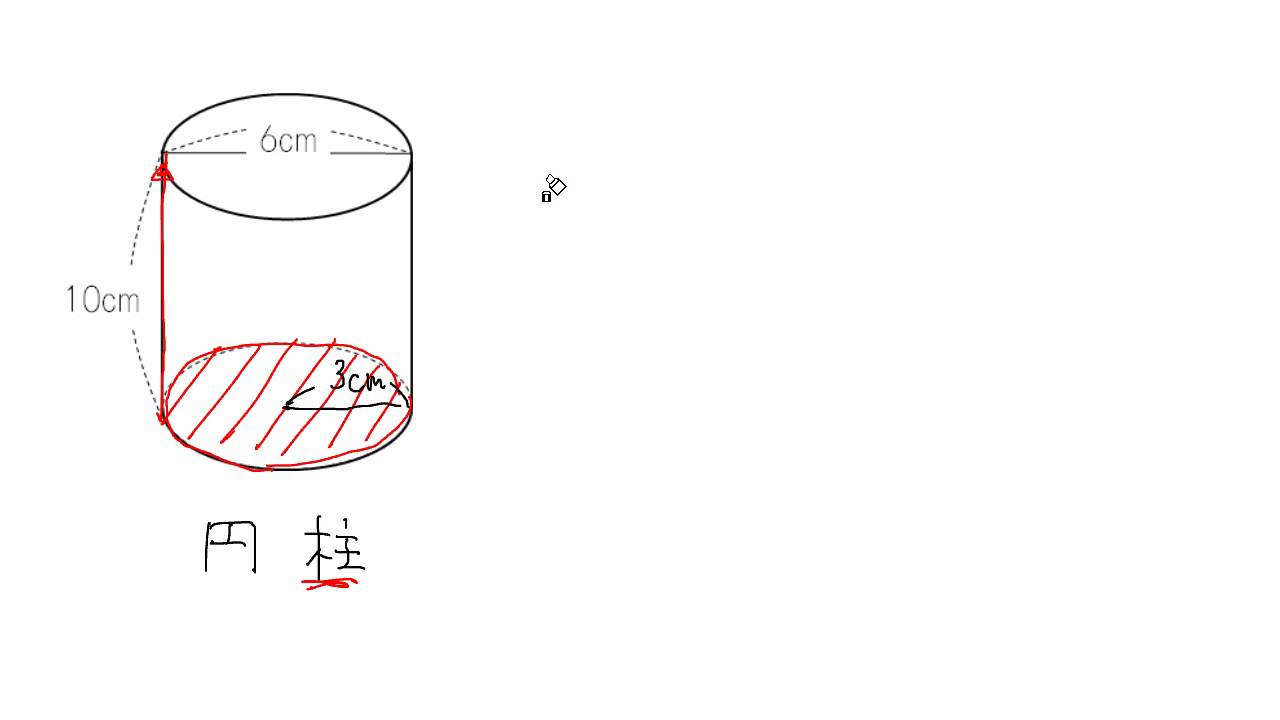



円柱の体積 Youtube




体積の求め方 計算公式一覧




円柱の表面積の求め方 公式と計算例




円柱の表面積 Youtube
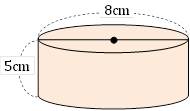



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




円柱の表面積と体積を求める公式 具体例で学ぶ数学




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト



1




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
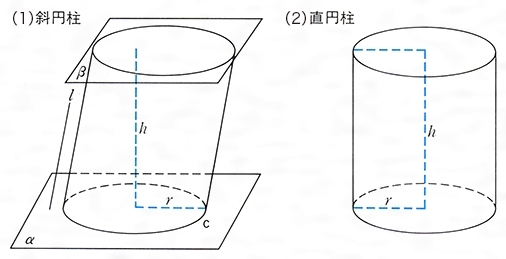



円柱とは コトバンク




初等幾何 球の表面積を求める 大人が学び直す数学




球の表面積と体積の公式 数学fun




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




角柱 円柱の体積 Youtube
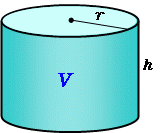



直円柱の体積 高精度計算サイト




円柱の表面積の求め方 公式と計算例
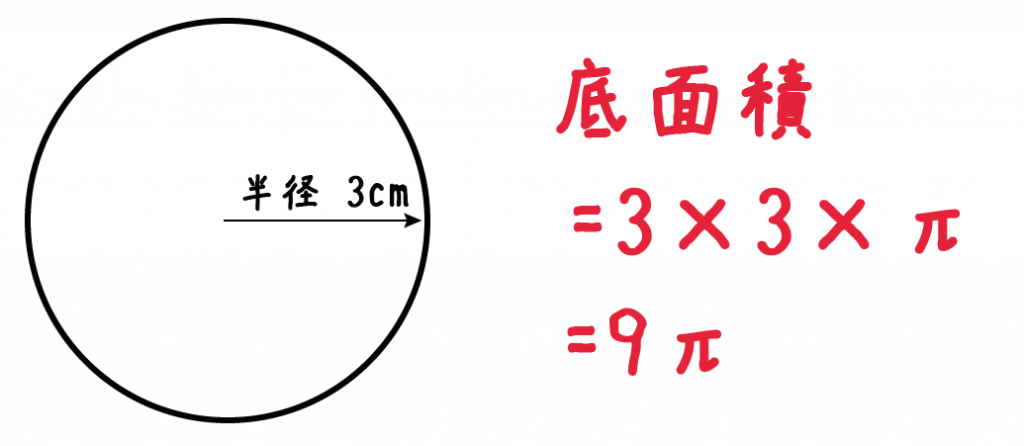



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積
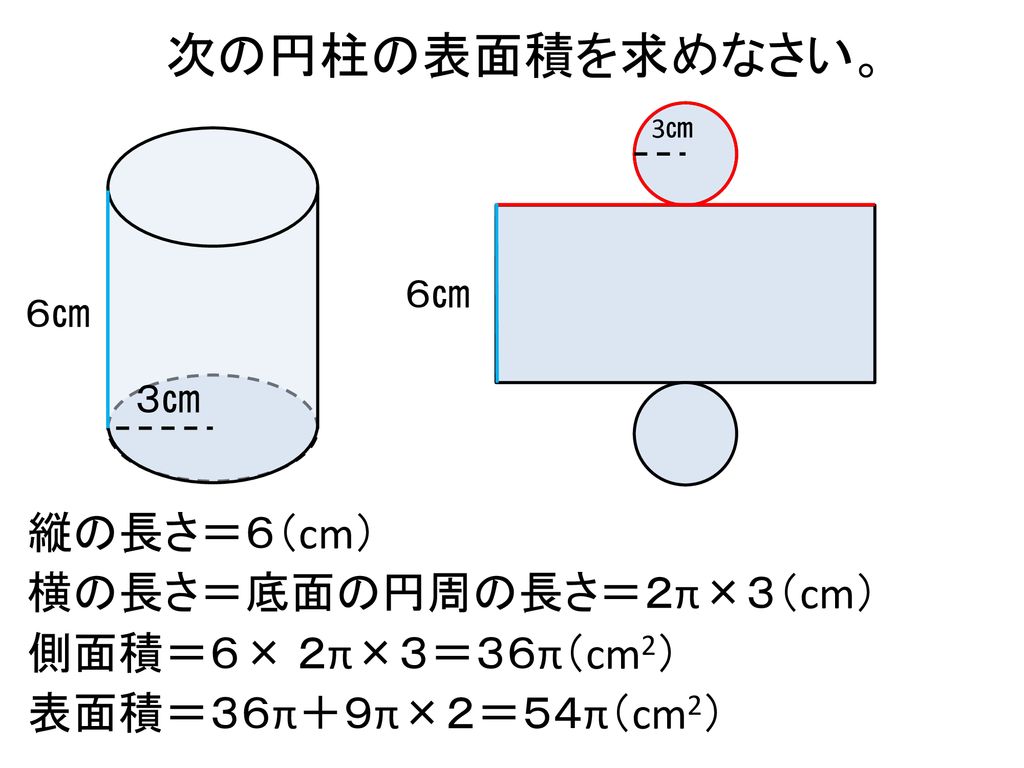



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download




円柱の表面積と体積を求める公式 具体例で学ぶ数学




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ
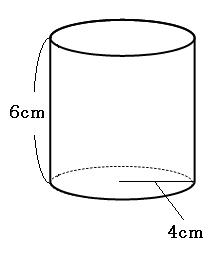



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
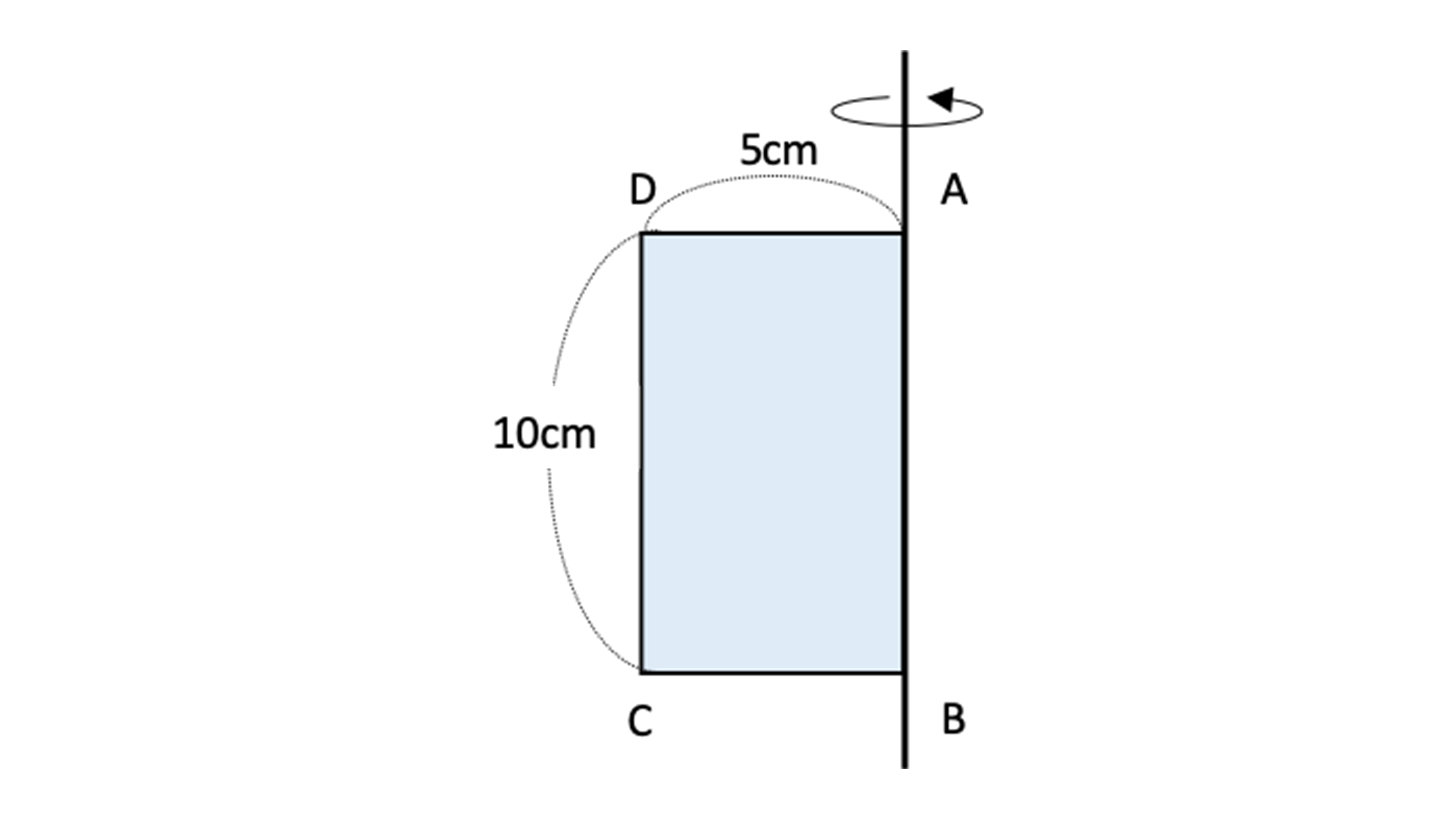



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち




球の表面積と体積の公式 数学fun




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




なぜこの円柱の問題の時 側面積の時2pをかけるのですか Clear




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
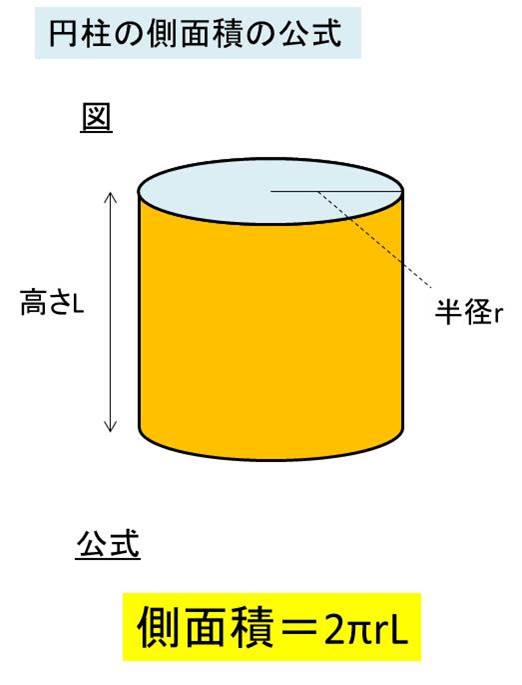



円柱の側面積 底面積 表面積を求める方法 モッカイ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角柱 円柱の表面積と体積の公式 数学fun



円柱の求め方について なんですが 小学校でやったはずの円柱の体 Yahoo 知恵袋



3



円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係
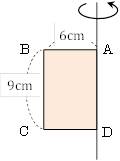



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
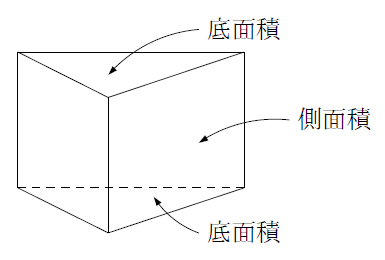



角柱 円柱の表面積 まなびの学園



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube



円柱の面積の求め方の公式を教えて下さい 半径 半径 P 円周率 Yahoo 知恵袋




中1 数学 6 2 角柱 円柱の表面積 Youtube




円柱の表面積の求め方 公式 小学生 中学生の勉強



5 8 円柱を3等分した図形の体積と面積を求めるには さんすうがく



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




球の表面積と体積の公式 数学fun




円柱の表面積の求め方 側面積の考え方をマスターしよう 中学数学 理科の学習まとめサイト



側面 側面積とは 問題を解いて慣れよう 苦手な数学を簡単に




円柱の体積の求め方 公式と計算例




円柱の表面積 Youtube




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ



3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




Catatan Tentang 体積 表面積 側面積 の公式 Junior Clear




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円柱の表面積の求め方の基本 現役塾講師のわかりやすい中学数学の解き方



円柱の表面積の求め方 公式 小学生 中学生の勉強



円柱の表面積 簡単に計算できる電卓サイト



円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係
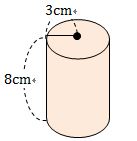



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




角柱や円柱の表面積の求め方を教えてください Clear




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
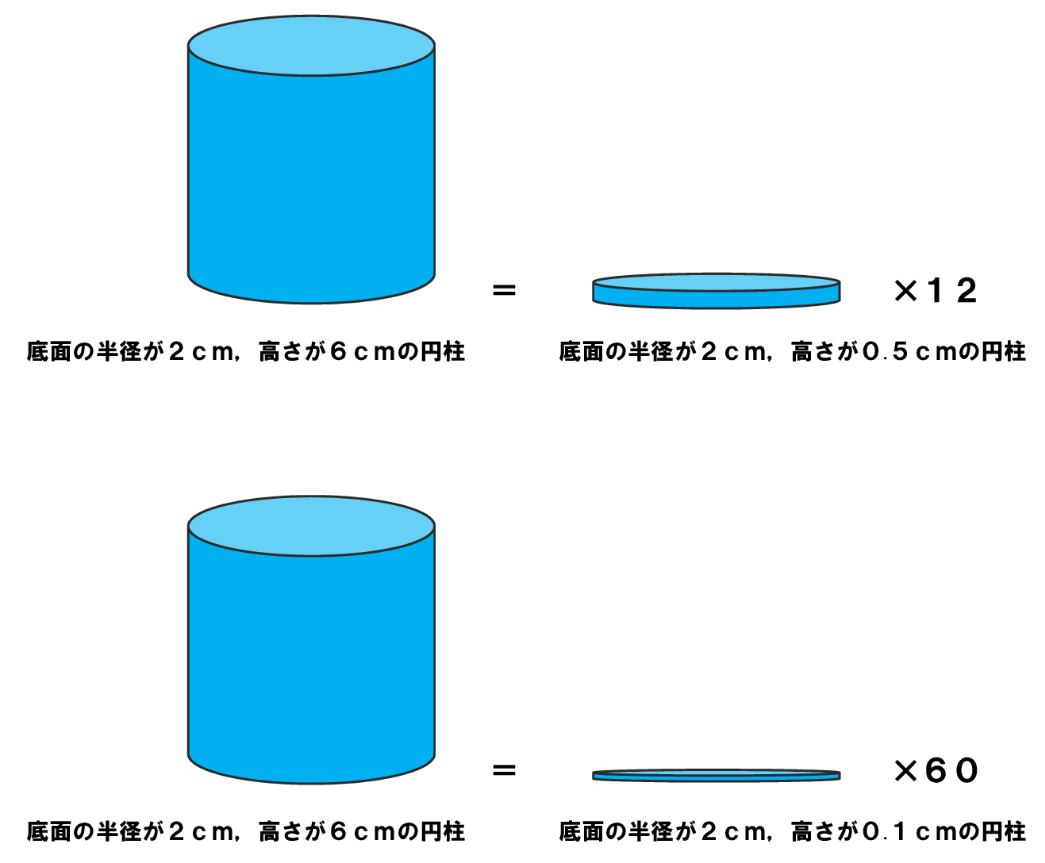



もたこ博士の算数工房 算数から数学まで




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



0 件のコメント:
コメントを投稿