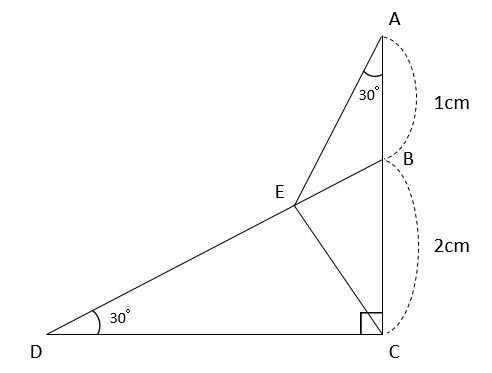
Ama04 練習問題へ abdu は直角二等辺三角形,u bcd は30 °,60 °の角をもつ直角三角形であるから,3 辺 のうちの1 辺の長さがわかると残りの辺の長さも求められる。 ここでは,共通のbd の長さを 調べると,xの値が求められる。 abhu とu ach に分けて,それぞれがどのような辺の比をもつ(追加アームと脚両端は直角三角形と2つの二等辺三角形、形成。 つまり、脚を直径とする半円と水平線との交点。) 5:4:3 比の威力 cf chebyshev linkage c 外人さんは、543 の直角三角形と気が付いていない様ですね。 直角二等辺三角形の辺の比は、必ず「\(\color{red}{1 1 \sqrt{2}}\)」 となります。 \(1\) 辺の長さからほかの辺の長さを簡単に求められるので、この比は必ず覚えておきましょう。

三平方の定理の二等辺三角形の比がありますが それを使うにはその図形の角度が写真のよう Clear
二 等辺 三角形 比
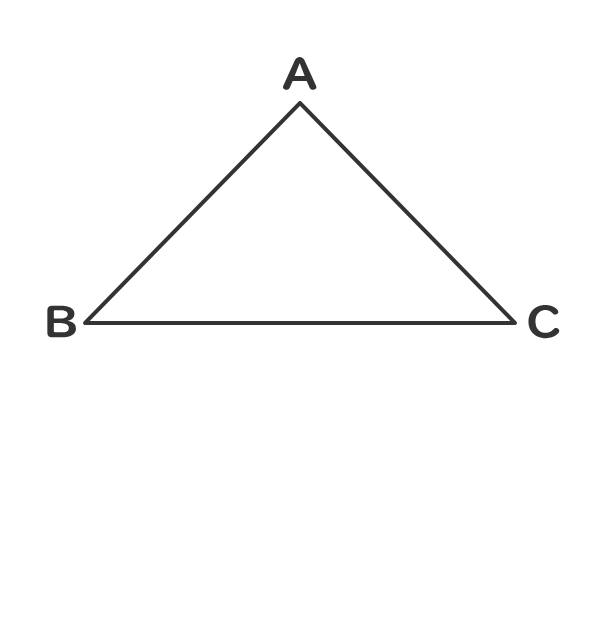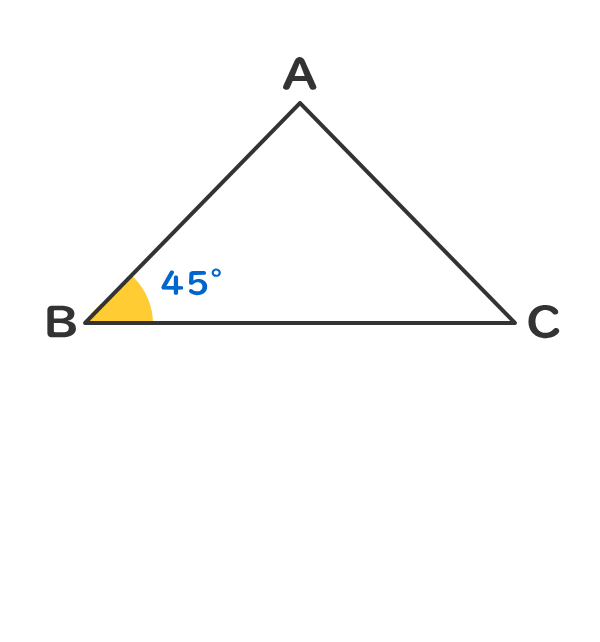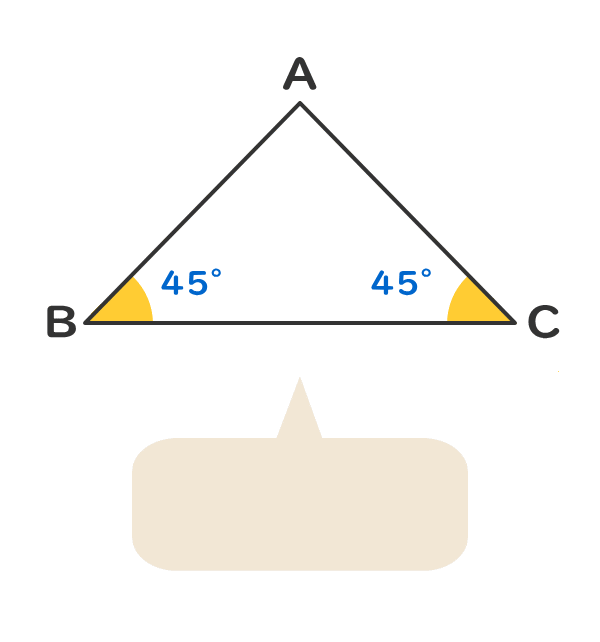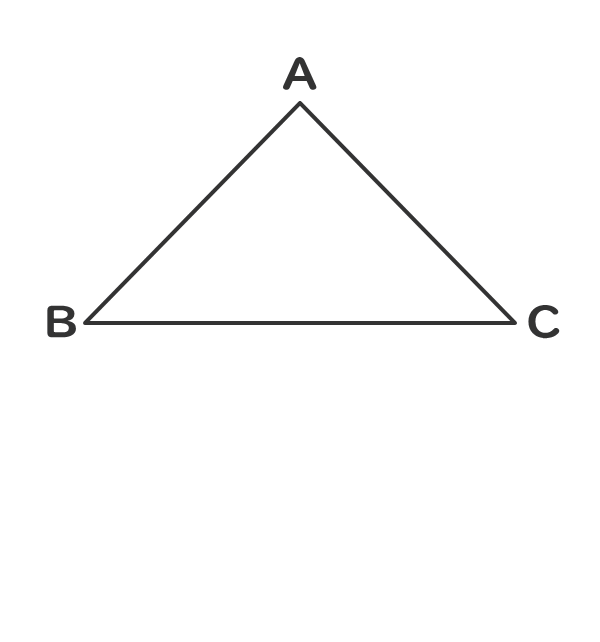
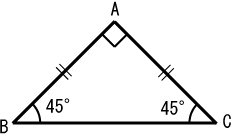
二 等辺 三角形 比-基本的な三角形と三角比 正方形の半分 直角二等辺三角形(各辺の比は 1 1 2) sin 45 ° = BC AB = 1 2 cos 45 ° = AC AB = 1 2 tan 45 ° = BC AC = 1 1 正三角形の半分 各辺の比が 1 2 3 の直角三角形 sin 30 ° = BC AB = 1 2 cos 30 ° = AC AB = 3 2 tan 30 ° = BC AC = 1 3 sin 60 ° = AC AB = 3 2 cos 60 ° = BC AB = 1 2 tan 60 ° = AC BC = 3 1となり、この三角形の辺の比は、見た目が最も美しいといわれる黄金比になっています。 問題 このように、2つの二等辺三角形に分割できる二等辺三角形の種類を全て求めてください。 3つの角が何度になるかを示してもらえれば、十分です。




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
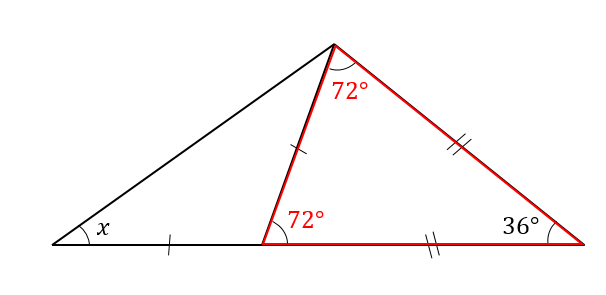
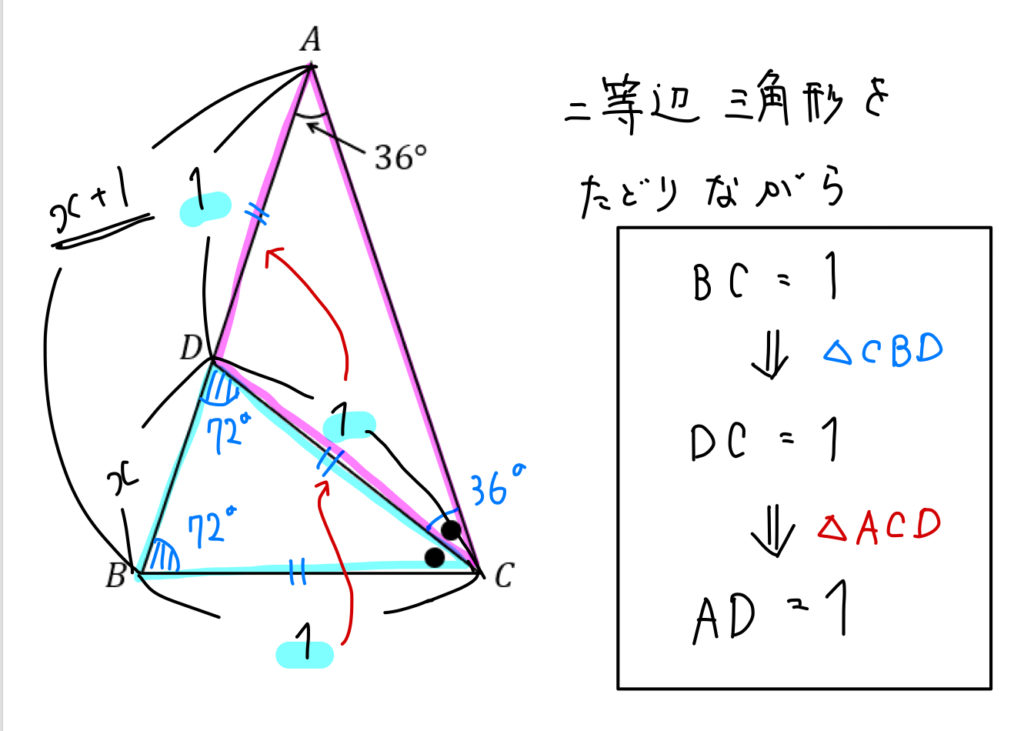
二等辺三角形の底辺は?1分でわかる意味、長さの計算、角度、高さ、三平方の定理との関係 底辺と高さが求められたので、あとは三角形の面積の公式を使うだけです。 こういう場合は、 分かる情報をどんどん書き込んでいきます。 14二等辺三角形の頂角の二等分線は底辺を 垂直 に二等分する。 三角形の 3 つの内角のうち(少なくとも)2 つの角が等しいものは、二等辺三角形となる(二等辺三角形の成立条件)。答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を
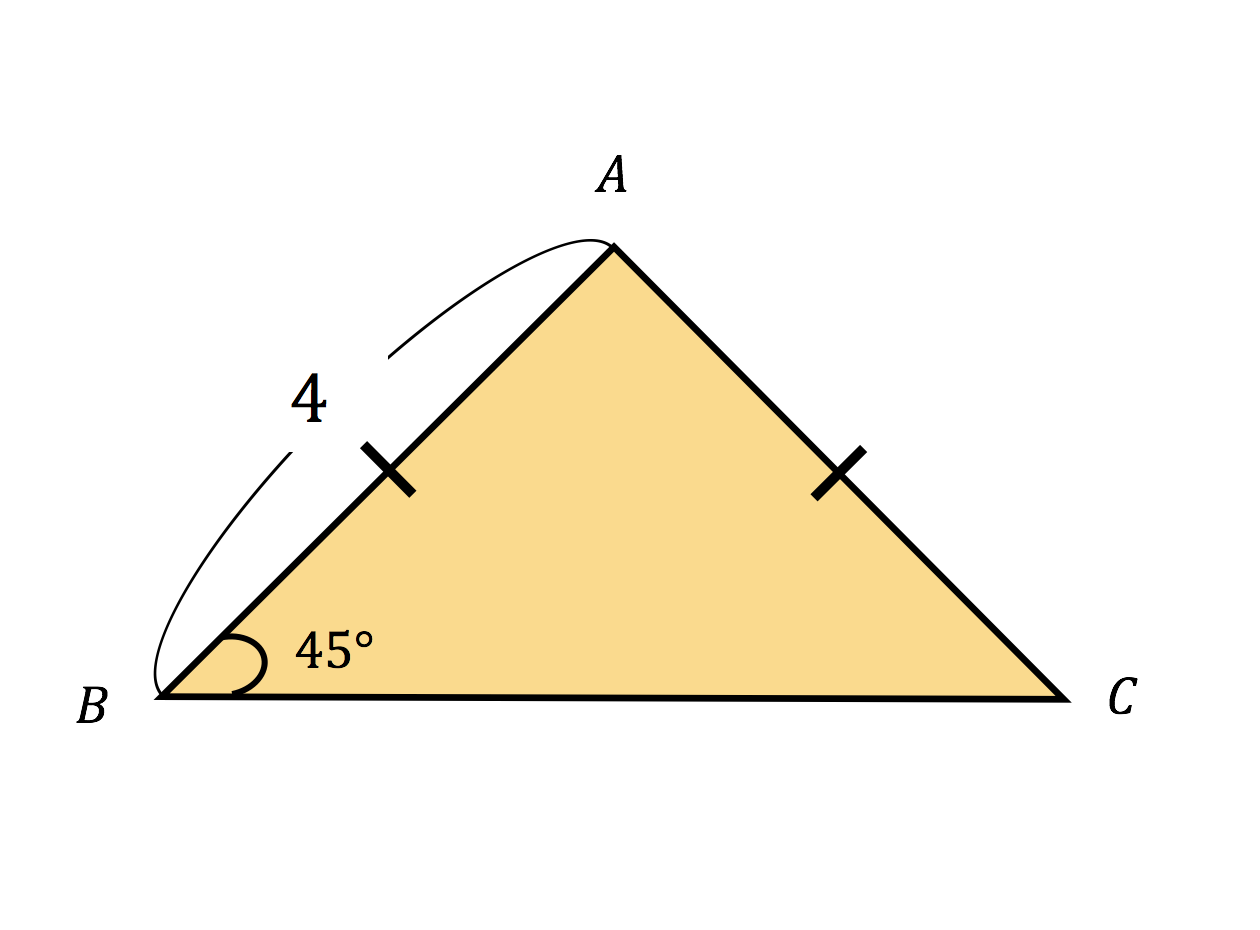
残りの辺はつぎの公式で計算できるよ。 斜辺をb、等しい辺の長さをaとすると、 a = √2b /2 で求められるんだ。 たとえば、 斜辺が4cmの直角二等辺三角形DEFがいたとしよう。 こいつの斜辺以外の長さは公式をつかうと、 EF = √2/2 × 4 = 2√2 cm①、②、③から、三角ACEは AE=AC -④ の二等辺三角形であることがわかる。 (※※2つの角が等しい三角形は二等辺三角形) 次にADとECは平行であるので BD:DC=BA:AE -⑤ (※平行線と線分の比}{ 11\sqrt{ 2 } }\)になります。 この辺の比を覚えておくことで、底辺から斜辺の長さを求めたり、またその逆のことができます。
図のように、12cmの辺に垂直に線を下ろすと、30°60°90°の三角形になりますので、辺の長さの比は②:①ですから、 2 となります。 (エ)は底角が15°の二等辺三角形ですが、このままでは面積は求めそして試験官も面倒くさいということで、 数値がキレイに出てくる三角比が問題にはよく出されます。 それは 角度が30°、60°、90°の直角三角形 と、 角度が45°、45°、90°の直角二等辺三角三角比の 45度 45度 90度の直角二等辺三角形、どこを底面にして高さにするかわかりません。 上と下どっちが合ってますか? ちなみに、下のlog3は、log1=0を用いて求めました。



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月
直角二等辺三角形の辺の長さは? 下図に直角二等辺三角形を示します。 斜辺以外の2辺が「等辺(辺の長さが同じ)」です。直角三角形の中でも、さらに特殊な三角形といえます。直角二等辺三角形の特徴は、 ・辺の長さの比が「1:1:√2」 ・角度が45度となり、この三角形の辺の比二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さここで、辺 AB 上に点 D を ∠CDB = 30 ∘ となるようにとると、 ∠DCB = 60 ∘ であるから、 ∠DCA = 75 ∘ − 60 ∘ = 15 ∘ である。 このとき、 ∠DCA = ∠DAC = 15 ∘ となるから、 △DCA は二等辺三角形とわか




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
次の直角三角形の辺の比は、 1 1 √2 だよ。 これは直角三角形の角度がそれぞれ、 45° 45° 90° の奴なんだ。 内角のうちの2つの角度が等しいから、 直角二等辺三角形 ってわけね。 辺の比を使ってやると、三平方の定理を使わずに辺の長さ出せるよ。愛光中−おうぎ形と三角形 21年 21年 5年生 6年生 おうぎ形 入試解説 共学校 四国 直角二等辺三角形 ★★★☆☆☆ (中学入試標準レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。 志望校への腕試しや,重要項目の二等辺三角形とは?定義・定理・性質や、辺の長さ・角度・面積・比の求め方、証明問題などを徹底解説! この記事では、二等辺三角形について、定義や定理、性質についてまとめていきます。 辺の長さや




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
この性質から二等辺三角形の内角の関係は 頂角(∠A)+底角×2=180° と表せ、つまり内角の角度がどこか1つでもわかれば全部わかるというお得な三角形ということがわかる。 (この二等辺三角形の性質が、あとでいろいろな問題を解く鍵になるのだ。) 念を押すように確認してみたがこれは全く難しくない。 説明されても躓かない(なにしろ一度通った道直角二等辺三角形befの面積は?(06年算数オリンピック、ファイナル問題より) 切断される立方体の個数は?(今年、18年 浦和明の星女子中学) この立体の体積は?(豊島岡女子学園中学 17年) 開いている?閉まっている?第233問 直角二等辺の辺の比 図形ドリル 直角三角形 直角二等辺三角形 相似 ★★★★★☆(算オリ・灘中受験生レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの




二等辺三角形 Wikipedia




よく使う三角比の値 数学i By Okボーイ マナペディア
直角二等辺三角形の選択入力値から他の要素の値を計算します。 h = a 2 b = a √ 2 L = ( 1 √ 2 ) a S = a 2 4 h = a 2 b = a 2 L = ( 1 2 ) a S = a 2 4 入力指定三角形の相似条件について図解で分かる相似条件 直角二等辺三角形とは?定義や辺の長さの比、面積の求め方 二等辺三角形 Wikipedia 二等辺三角形の性質と辺の長さの求め方!押さえておきたい三 ここでは、二等辺三角形の辺の長さ、角度、面積、比の求め方を例題を使って解説していきます。 例題 \(\mathrm{AB} = \mathrm{AC}\)、頂角が \(1^\circ\)、\(\mathrm{BC} = 8\) の二等辺三角形 \(\mathrm{ABC}\) があります。



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




この公式は角度が1のときだけ使えるのですか Clear
直角二等辺三角形 直角(90度)以外の二つの角度は45度 。 正三角形と直角三角形 正三角形はすべての角度が60°。 正三角形を半分にすると「30°、60°、90°の直角三角形」になり、 一番長い辺が一番短い辺の2倍の長さになる 。 三角形の面積の公式―底辺×三角形と比の定理 したがって efgは二等辺三角形となる。 確認 四角形abcdで、p,rはそれぞれ辺ad, bcの中点、q,sはそれぞれ対角線bd,acの中点である。 答表示 a b 二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な




黄金三角形による18 シリーズの三角比 おいしい数学



数学について質問があります 三角比 問題 二等辺三角形a Yahoo 知恵袋
第25回 三角比を使う NHK;直角二等辺三角形の辺の長さの比は 1 1 √2 でしたから、 と分かります。三平方の定理の応用 三平方の定理が成り立つ整数の組 三平方の定理は、平方が登場してくる関係上どうしてもルートが出てきやすくなってしまいます。 その 三角形の角の二等分線と線分の比 三角形の性質の一つに、こんなものがあります。 {ace}$は二等辺三角形である。 そのため、2つの三角形の面積比は底辺の比である。直角二等辺三角形の「斜辺だけ」わかってる場合だ。 このとき、 残りの辺はつぎの公式で計算できるよ。 斜辺をb、等




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



3
は黄金比φ 2 5 1 の逆数 であるから,内接円の半径が最大となると き,等辺:底辺 φ:2 である.黄金比が 最も美しい比であると言われるが,それに 倣えばこの比の二等辺三角形が最も美し い二等辺三角形であると言えるのだろうか.確かに,安定感を直角二等辺三角形比, 直角二等辺三角形の辺の長さは?1分でわかる求め方、 直角二等辺三角形の辺の長さは?1分でわかる求め方、公式、辺の長さと角度の関係、証明 無料サンプルあり!一級建築士対策にも使えるお得な用語集はこちら⇒ 全77頁! 二等辺三角形ではない三角形を思い浮かべてください。 いろんな三角形が思い浮かんだと思いますが、その中に正三角形はありましたか? ないですよね? すなわち 二等辺三角形ではない ならば 正三角形ではない これは今、想像してもらった通り真です。



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




7 Abcab Ac A See How To Solve It At Qanda
この問題に答えるためには,辺の比が1: で,その間の角度が45°のときは,「1:1: の直角二等辺三角形になる」という中学校数学の基本が前もって分かっていなければなりません. このことに気づかない場合は, などと,ab間の距離も求める必要があります.三角形の形状問題(正三角形,二等辺三角形,直角三角形など三角形の種類を言い当てる問題)や証明問題においては,正弦定理や余弦定理を変形して,角度に関する式を辺に関する式に直してから考えるのが原則です. ・ tan A は上記2つを用いてとします三角比 とは、直角三角形の3つある角の90度以外のどちらか1つの角度が決まれば、3つの辺の長さの比率が決まるという性質のことです。 注意:直角二等辺三角形の場合は角度が決まらなくても3辺の比率は決まってしまいます。 三角比として頻繁にでてくる角度は、 30度と45度と60度 です。 中学生では、この3つの角度の時の三角形の比率を全て覚えておけば、数学の




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




黄金三角形 Wikipedia




三角比15ºと75º 数式で独楽する
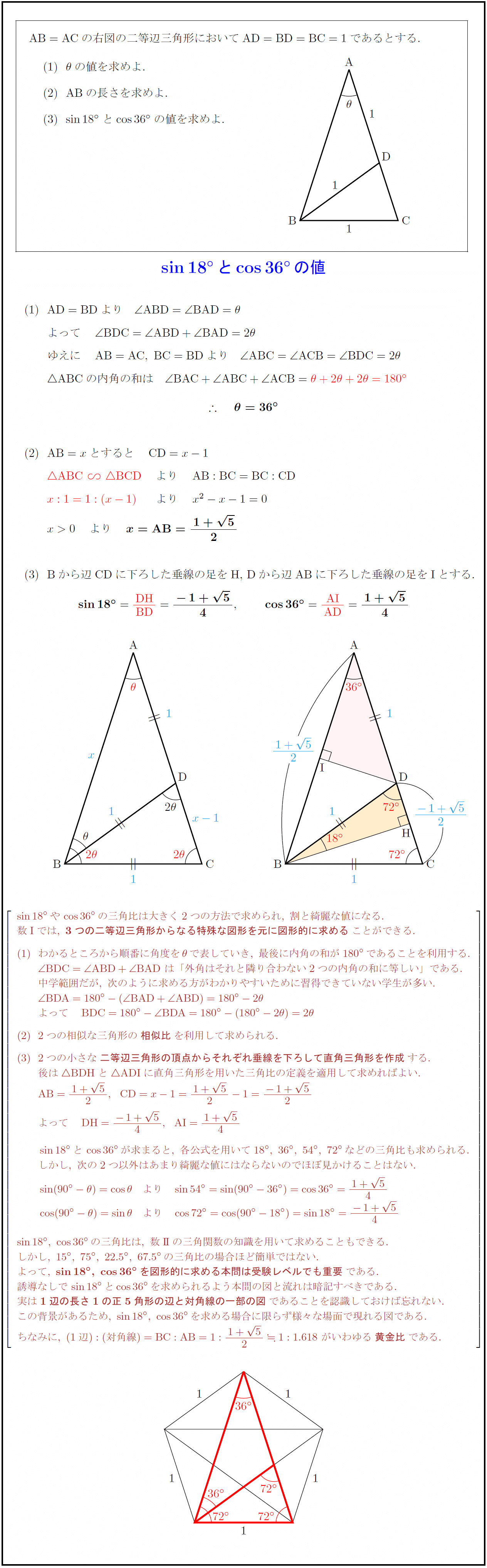



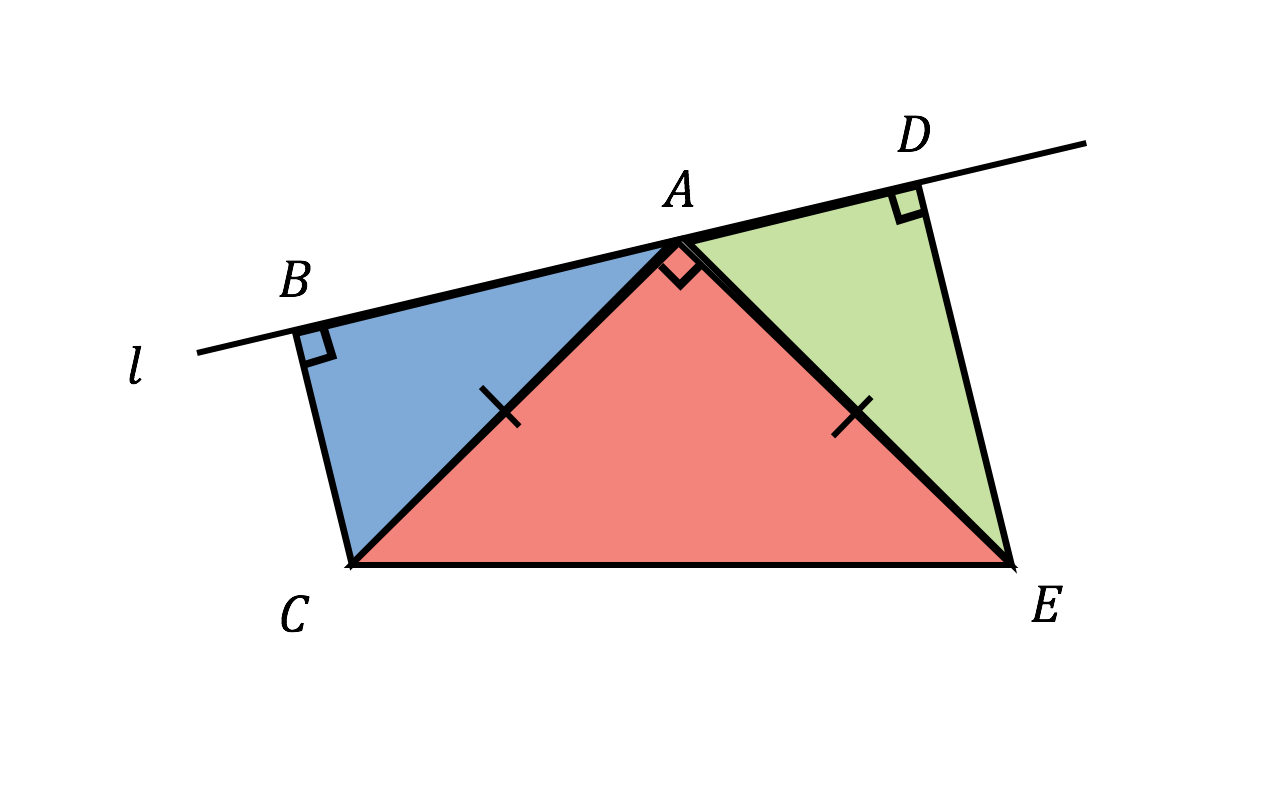
高校数学 Sin18 とcos36 の値 正五角形を利用した図形的解法 受験の月




36 72 などの三角比 数学i フリー教材開発コミュニティ Ftext




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学



画像で三角比を使わずに角abcを求める方法がわかりませんヒントは直角二 Yahoo 知恵袋
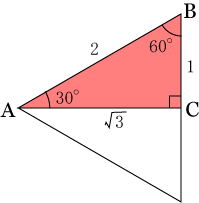



基本三角形と三角比



三角形の種類を判定しよう 電験3種web
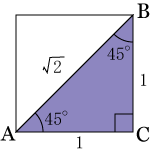



基本三角形と三角比




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




二等辺三角形の面積を求める算数の公式は




黄金三角形による18 シリーズの三角比 おいしい数学




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア




数学の内心の問題です 1 1 2の比の直角三角形の内接円の半径が1セン 数学 教えて Goo



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく



1




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう



二等辺三角形の各辺の比について質問です 二等辺三角形の Yahoo 知恵袋



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に
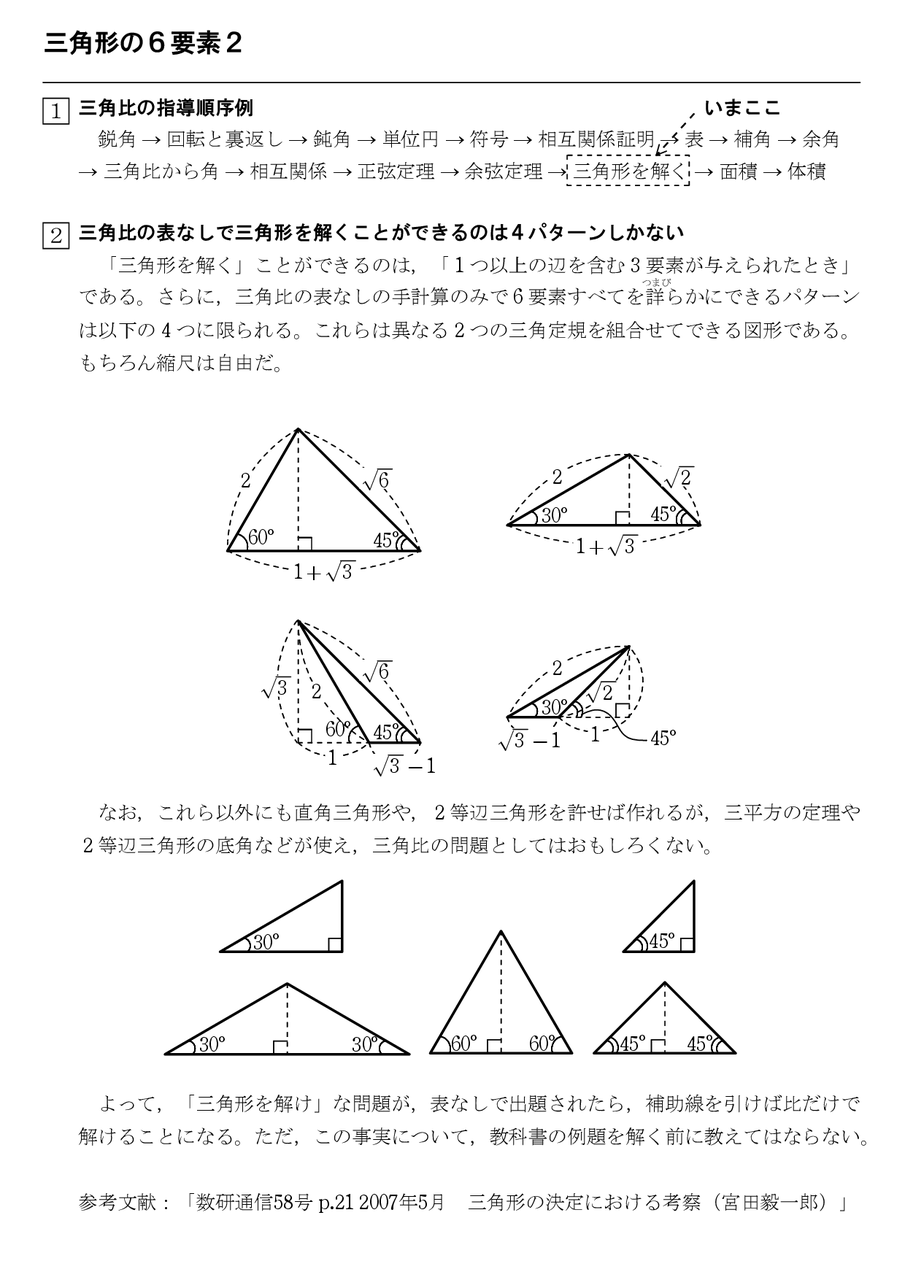



三角形の6要素2 怜悧玲瓏 高校数学を天空から俯瞰する




黄金三角形による18 シリーズの三角比 おいしい数学
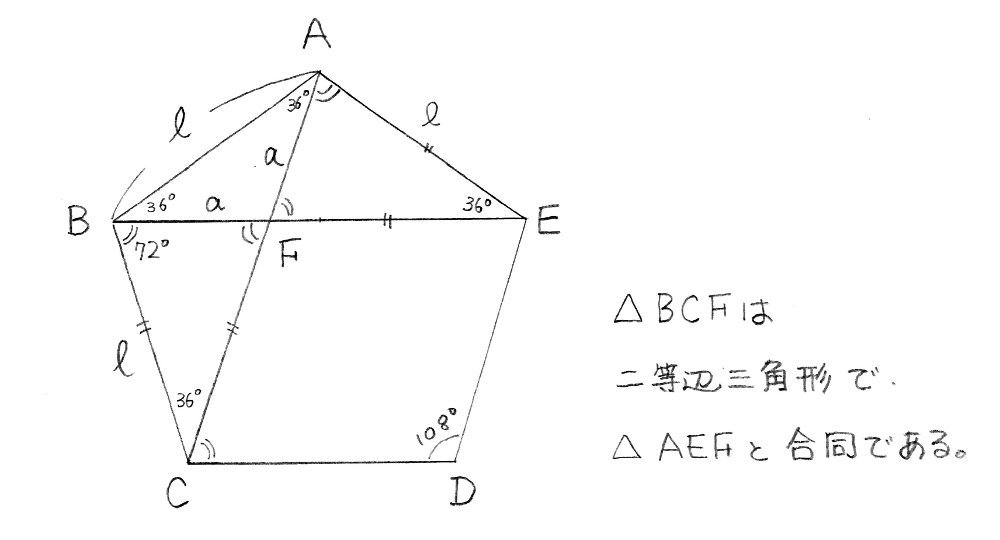



五角形5 辺と対角線の比 Wandering In The Woods




二等辺三角形の性質の証明 頂角の二等分線 Youtube




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
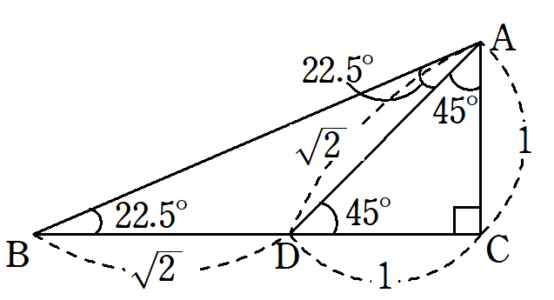



22 5 の三角比 Fukusukeの数学めも




15 シリーズの三角比 おいしい数学




三平方の定理の二等辺三角形の比がありますが それを使うにはその図形の角度が写真のよう Clear




三角比 30 45 60 もう一度やり直しの算数 数学




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




無料印刷可能直角二等辺三角形 比率 最高のぬりえ
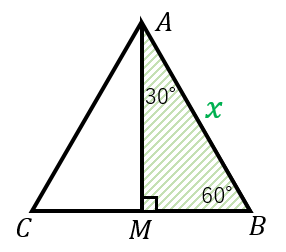



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明



二等辺三角形の 3辺の長さの比率は同じですか 例えば 一番小さい角の角 Yahoo 知恵袋



二等辺三角形の分割




スタディピア 図形




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




9 Ab4c Abc Dc B9 C P10 A Descubre Como Resolverlo En Qanda



1




三角形の問題 平行 二等辺三角形 問題 三角形abcにおいて 角bの二 Okwave



1
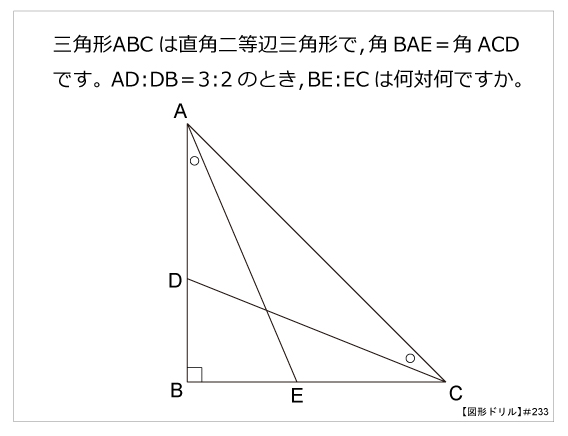



図形ドリル 第233問 直角二等辺の辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦
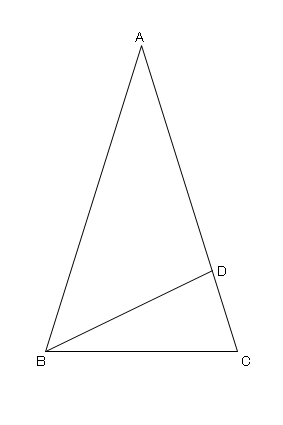



三角形の相似の証明 2 ネット塾




テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア



相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室
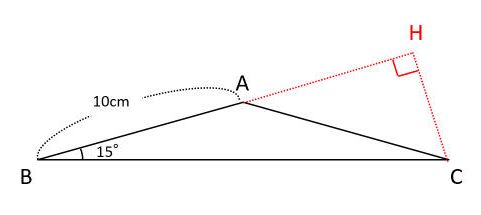



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ



直角二等辺三角形 Wikipedia




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
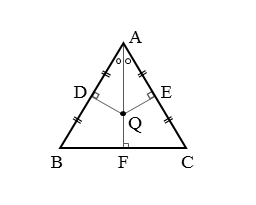



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん




1 はどうして二等辺三角形の辺の比1 1 2 を使えないんですか Clear




二等辺三角形の性質 Youtube




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




白銀比三角形を見ていて気付いたこと 大したことない Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー



二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




三平方の定理 覚えること 三角定規 苦手な数学を簡単に
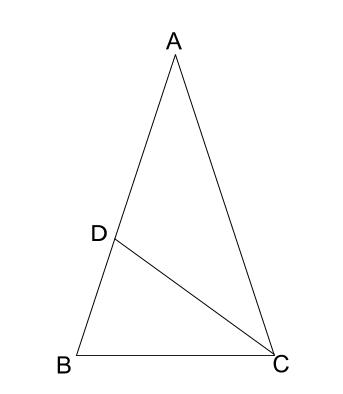



中学数学 相似と方程式 中学数学の無料オンライン学習サイトchu Su



直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題



Math Battle 0075 一辺を共有する二等辺三角形
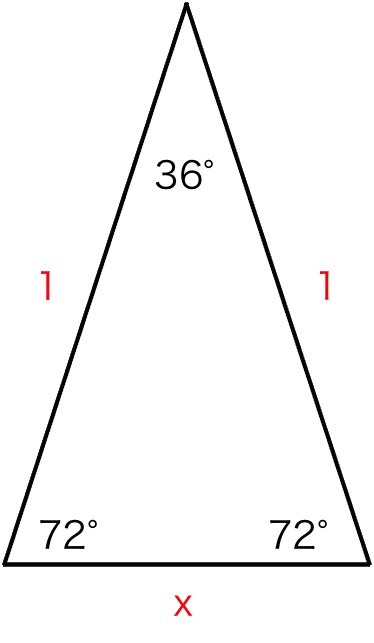



18 36 72 などの三角比 5角形 10角形 黄金比 社会人になってからのスキルアップ




今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




なぜ三角形cdeは直角二等辺三角形だとわかるのかが理解できません 教えてください Clear




原田 浩明 Sサクシード296 頂角36 の二等辺三角形 正五角形 15 75 の三角比 高校 数学i 三角比
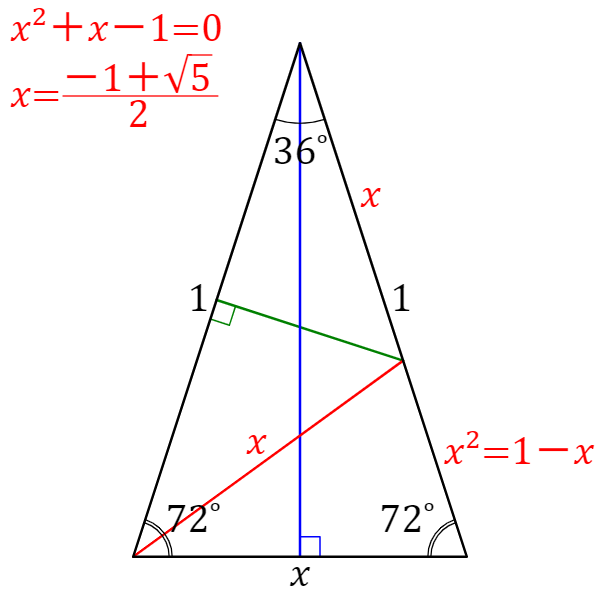



Sin18 Cos72 Cos36 Sin54 を簡単に求める方法 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




応用 36度の三角比 なかけんの数学ノート
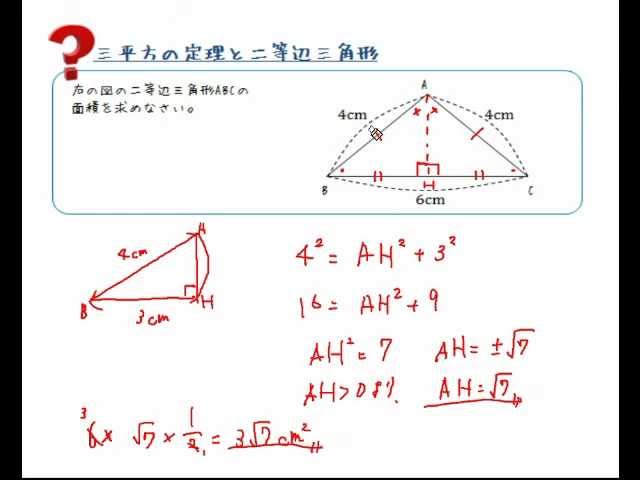



三平方の定理と二等辺三角形 Youtube




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



高校入試 英語 数学 特別な直角三角形




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo




二等辺三角形の角を求める Youtube




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
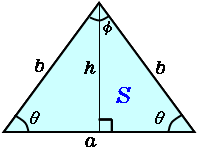



二等辺三角形 高精度計算サイト



0 件のコメント:
コメントを投稿