N a 2 4 cot π n {\displaystyle {na^ {2} \over 4}\cot {\pi \over {n}}} と求められる。 この式は、正 n 角形の外心から、各頂点に向けて、線分を引き、 n 個の二等辺三角形に分割することで容易に証明できる。 (それぞれの二等辺三角形の高さが a 2 cot π n {\displaystyle {a \over 2}\cot {\pi \over {n}}} とな · カンタン公式扇形の中心角の求め方がわかる3つのステップ 扇形の中心角の求め方の公式を知りたい! こんにちは、この記事をかいているKenだよー!豆乳ラテだったら3杯はいけるね。 「扇形の中心角の求め方」の公式 ってチョー便利。多 角形 の 求め 方 頂点座標 中心点 cos 角度 図形の大きさ とで得られる多角形を星型多角形という星型多 角形では内部にある多角形の各辺を延長してで きる角だけを内角とする ②星型多角形の種類 星型多角形では点を何点とばしで 両 角 宗 晴* 1
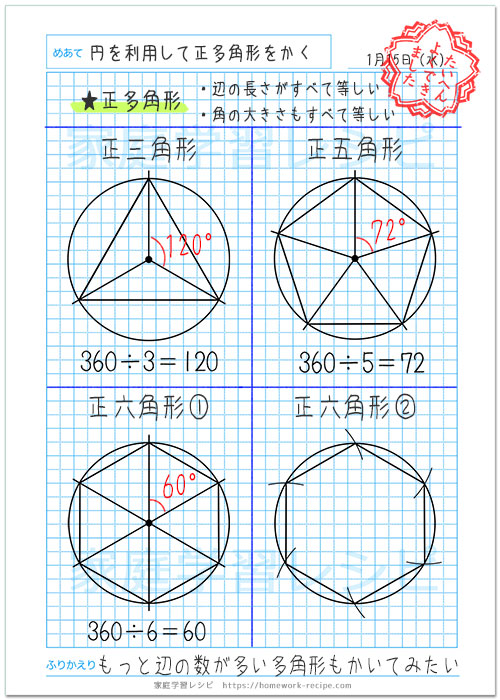
円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ
多角形の角度の求め方
多角形の角度の求め方-多角形の内角の和の公式と外角の和を利用した角度の求め方 底辺と高さから角度と斜辺を計算 高精度計算サイト 「三角形の内角の和が180°なのはなぜ?」小学生に教えるため 星形の角度内角の和の求め方を問題解説! 数スタ図では隣り合っている赤と青のそれぞれが1組180 です� 正十二角形に図のように対角線を引くと、12-2=10個の三角形に分かれます。 だから、正12角形の一つの内角は、180 ×10÷12=150 です。 空色二等辺三角形のとんがった方の角の大きさは、150 -2×6




内角の和 180 N 2 外角の和 360 教遊者
· さて、具体的に角Aの余弦、つまり\(\cos A\)を求めてみます。 公式の使い方ですが、実は頭の中では次のように考えて使います。 求めたい角度の対辺はどれか? 求めたい角度を挟んでいる辺はどれか? もし、求めたい角がAであるのなら、 対辺はa、多角形(四角形・五角形・六角形・・・)の内角の和の公式&問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されます。正多面体の頂点と辺の数の求め方を教えて Yahoo!知恵袋 簡単公式多角形の対角線の本数が5秒でわかる求め方 sinを用いた三角形の面積公式 高校数学の美しい物語;
★無料の中学メルマガ講座★毎週、問題と動画講義をお届け! 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料04 · 外角・内角の和、面積、対角線の本数の公式と求め方 21年2月19日 この記事では、「多角形」の種々の公式(外角の和・内角の和、面積、対角線の本数など)やその求め方をわかりやすく解説していきます。 また計算問題の解き方もわかりやすく解説して · 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180× (52)/5 = 108°
· まず、外角1つ分の大きさを求めて 180°から外角1つ分の大きさを引いてやります。 先ほど外角の求め方のところで 1°になるということがわかっているので 正三角形の内角1つ分の大きさは $$\large{1801=60°}$$ となります。 正五角形の場合Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2)<三角形の内角・外角> <角度の意味> <三角形の3つの角の和の求め方> 360° 180° (小学校の方法) 図形の学習をしてこなかった,あるいは,学習の経験が不足し ているために,三角形や四角形,辺や角(角度)の概念が理解で




数学 中2 53 角度チャレンジ Lv 1 Youtube
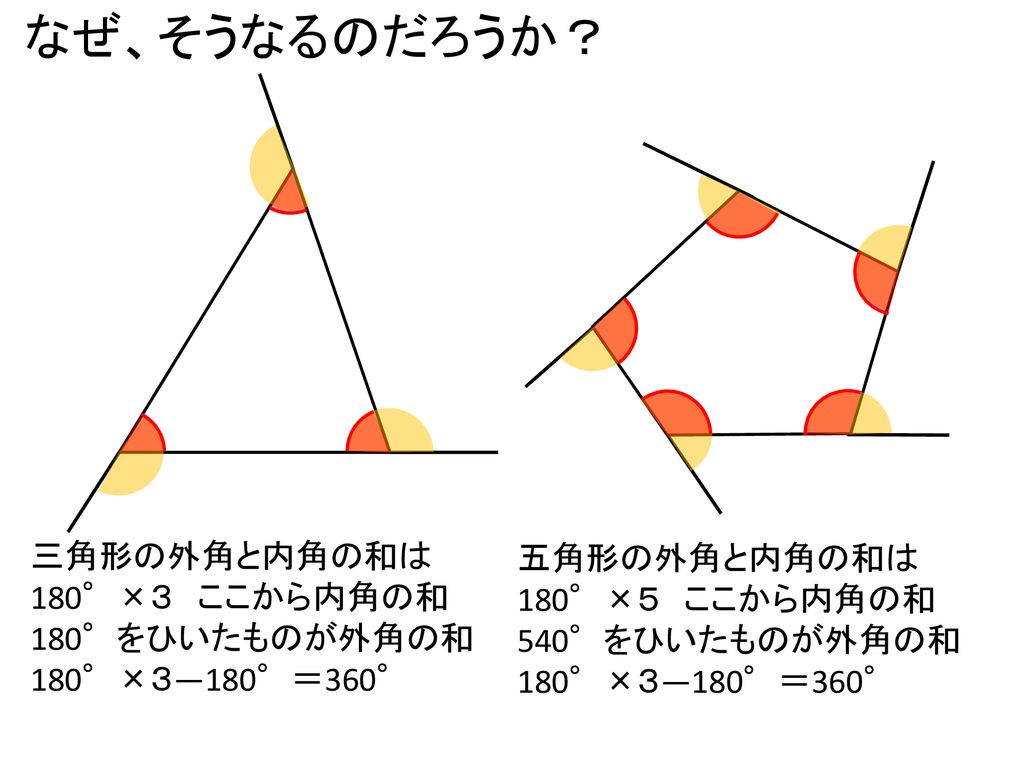



多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download
円周率の意味や求め 方を理解し,円周の 長さを求めることが できる。 円周の長さは直径の 長さに比例している ことを理解する。 「円周率」の意味を知り,その求め方をまとめる。 「算数のおはなし」を読み,円周率についての歴史に関心をもつ。 · 直角三角形ahcにおいて、三平方の定理を使うだけです。 ac=√(ah^2ch^2) =√(4864) =4√7 となり、対角線の長さacが求められました。 多角形の対角線の本数の求め方 多角形の対角線の本数は、いちいち引いて数えなくても公式を使って一瞬で求められます。また、図形の内側の角を内角といい、それから延長した辺と1辺がつくる角を外角といいます。 この2つの角度を足すと 180° になります。 多角形の内角の和を測ってみよう! 多 角形 の 求め 方 頂点座標 中心点 cos 角度 図形の大きさ
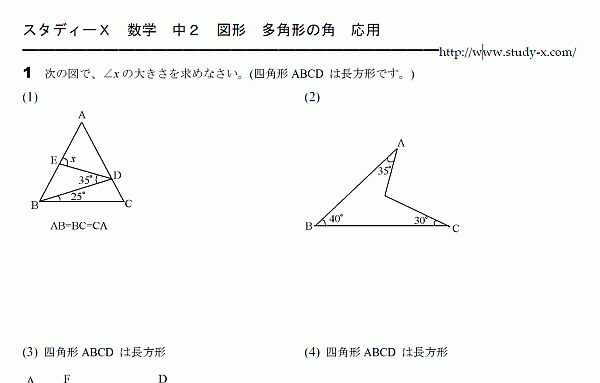



多角形の角 応用 無料学習プリント教材
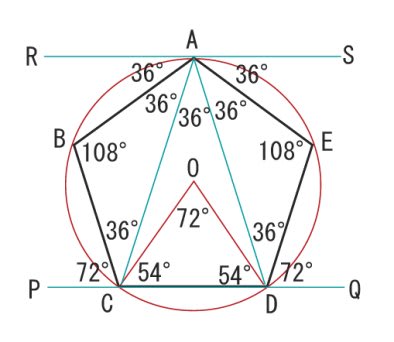



正五角形というだけで 分かる角度は 名寄 算数数学教室より
学 5 全体の場でそれぞれの考え方を発表し, いろいろな方法の中から,簡単な求め方を び 話し合う。 考えさせる。 合 三角形の角の大きさの和が180°であること い を用いると,簡単に求められることをつかま せる。 「全体の前での説明する様子」180× (5-2)-180×5 +180× (5-2)=180° 点Aを通るBE,CE,BDとの平行線を引き,錯角の関係でa~eの5つの角を点Aに集めることができ,一直線になるので,180° 点A,C,Dを通るBEとの平行線を引き,錯角の関係でa~eの5つの角を点Aに集めることができ,一直線になるので,180° 外側の五角形から,付け足した三角形5つ分の印を付けた角の和 (五角形の外角の和)を引くと,① 十二角形の内角の和を求めよ。 ② 正九角形の一つの外角は何度か。 答①1800° ②40° 内角の和、外角の和 例題と練習問題 例題 三角形の内角と外角の関係 印をつけた角の和 角の二等分線と内角の和 練習問題 角度1 角度2 角度3




内角の和 180 N 2 外角の和 360 教遊者
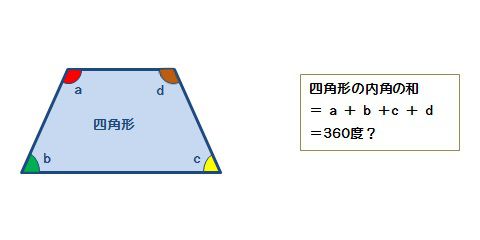



四角形の内角の和 算数の公式覚えてますか
問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答三角関数の角度を計算する場合、「エクセル」を使うと便利です。 θ=Arcsin (038)のような半端な辺の比に対する角度も計算できます。 まずエクセルのセルに「= ASIN (038)」と入力してください。解説 ≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
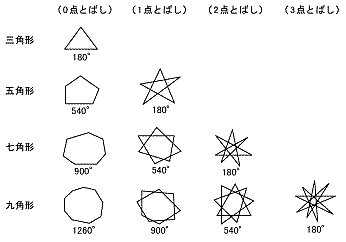
S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2) i f a ≥ b, c h = 2 S a, B7角形の重心を計算しよう。 計算上、最後の3角形の面積計算のため、1番目の点座標を8番目にも設定します。 図4 多角形(ポリゴン)の重心計算 簡単ですね。点の結び方 星形五角形 星形六角形 星形七角形 星形八角形 星形九角形星形十角形 角の和の公式 単位:度(°) 180° 360° 540° 7° 180° 360° 540° 180° 360° 7° 900° 1080° 180n-360×2 =180(n-4) 180n-360×3 =180(n-6) 180n-360×4 =180(n-8) p番目 ごと 180n-360×p =180(n-2p)



中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題
(2) 星型多角形のつくり方 ①星型多角形とは いくつかの点を何点かとばして結んでいくこ とで得られる多角形を星型多角形という。星型多 角形では,内部にある多角形の各辺を延長してで きる角だけを内角とする。 ②星型多角形の種類角度や面積を求める(多角形の性質)解き方と問題一覧 右の図で, x の角の大きさは何度ですか。 (図は解説の中) 正八角形の1つの内角の大きさは何度ですか。 右の図の,印をつけた7つの各の合計は何度ですか。 右の図の五角形ABCDEは正五角形です。 また,直線アと直線イは平行です。 ・・・・ (1) 正五角形ABCDEの1つの内角の大きさは何度ですか。Bn1 = q an1bn とすれば、an、bn はそれぞれ直径1の円に外接、内接する正6¢2n 角形の長さになり ます。
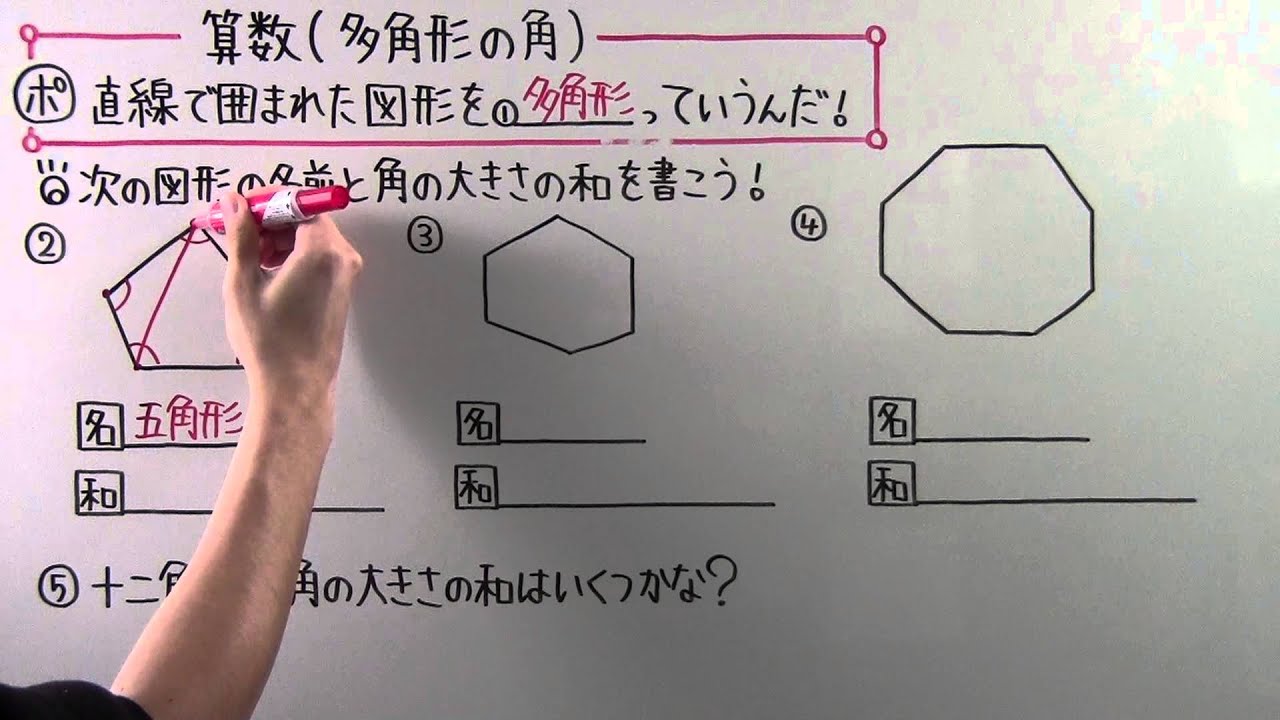



小5 算数 小5 33 多角形の角 Youtube




多角形の性質 中学受験準備のための学習ドリル
・友だちの解き方を聞くことによって,問題解決の糸口になった生徒が多い。 <発表された生徒の解き方> 第2時 (1) 新しい問題を設定させる。 (2) 各自で問題に取り組ませる。 ・自分でつくった星形多角形の頂角の和を求めてみよう。2907 · 2 円周率計算の基本となる公式 21 正多角形による方法 円周率の古くからの計算法は正多角形で円を近似する方法です。 a0 = 2 p 3, b0 = 3 として an1 = 2anbn an bn;このように、順次求めていく事により、 各点(節点)における方向角が求められ る。 <方向角に関する例題> 以下に、h91d の問題を例に挙げ、方向角の計算を確認する。 図のような多角測量を実施し、表の観測値を得た。
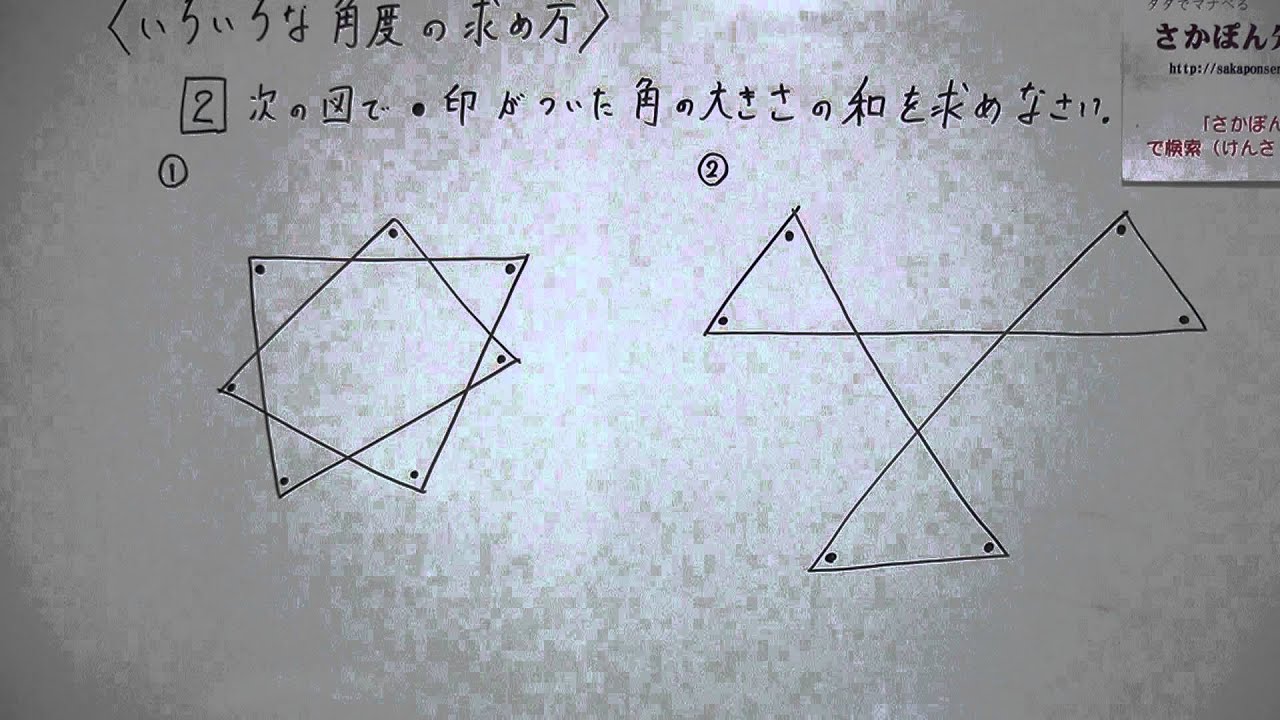



中学校2年生数学 いろいろな角度の求め方
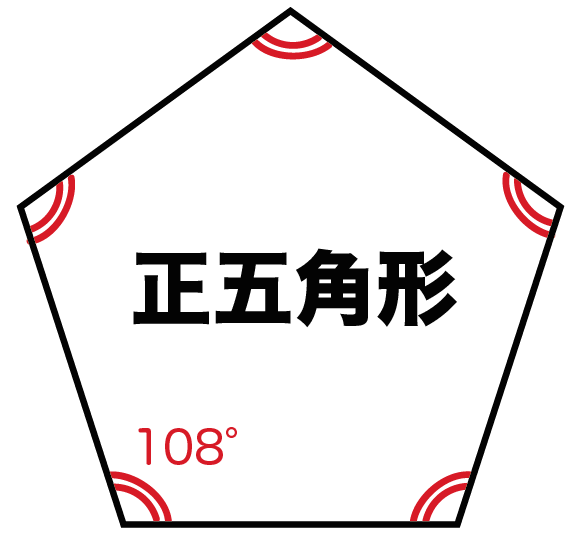



正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
· 証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説! 正三角形の角度 正方形、ひし形との融合問題を解説! 平行四辺形と授業では、作図をして角度を求めさせ、 頂角の和が1800であることを多様な方 法で証明させた。かなり難しい内容なの で、6種類のヒントプリントも用意して、 理解の促進を図った。様々な証明方法の 存在に生徒も紫いていた。・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数 ・角度から三角関数 角度(度またはラジアン)から三角関数を計算します。 ・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。
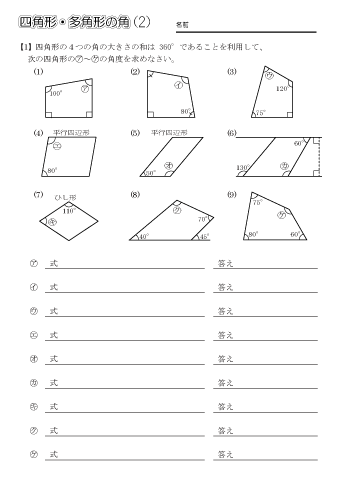



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
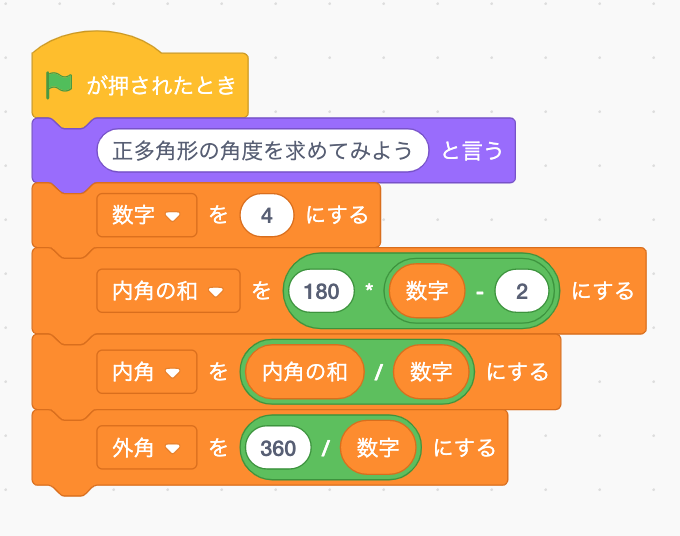



Scratch プログラミングで正多角形の内角 外角を求めてみよう いなきたものづくりラボ
この問題を見て,逆三角関数 tan1 (C言語では atan() や atan2()) を使って CP と CQ の角度をそれぞれ求め, 両者を比較しようと考えた方が多いのではないでしょうか. しかしこの問題では,角度そのものではなく角度差の符号を求めればよいので, 逆三角関数を使う方法よりも簡単で優れた,外積(1)下の図について,ア,イの角度を求めなさい。 ① ② (2)下の図の三角形について,ウ,エの角度を求めなさい。 ① ② (3)下図の平行四辺形ABCDについて,オ,カの角度を求めなさい。 (4)下の図の二等辺三角形について,キの角度を求めなさい。 · 高校までの範囲ならば、辺の長さが実数で与えられているはずなので特殊な角度だけ覚えておけば大丈夫だと思います。 arctan 0 = 0 arctan 1/√3 = π/6 arctan 1 = π/4 arctan √3 = π/3 (2) 辺cの値を求めます。 直角三角形であるので、 c = √ (a^2 b^2) となります。 cosθ1 = a/c より、 θ1 = arccos a/c となります。 また、 cosθ2 = b/c より θ2 = arccos b/c となります。 (1)と




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ
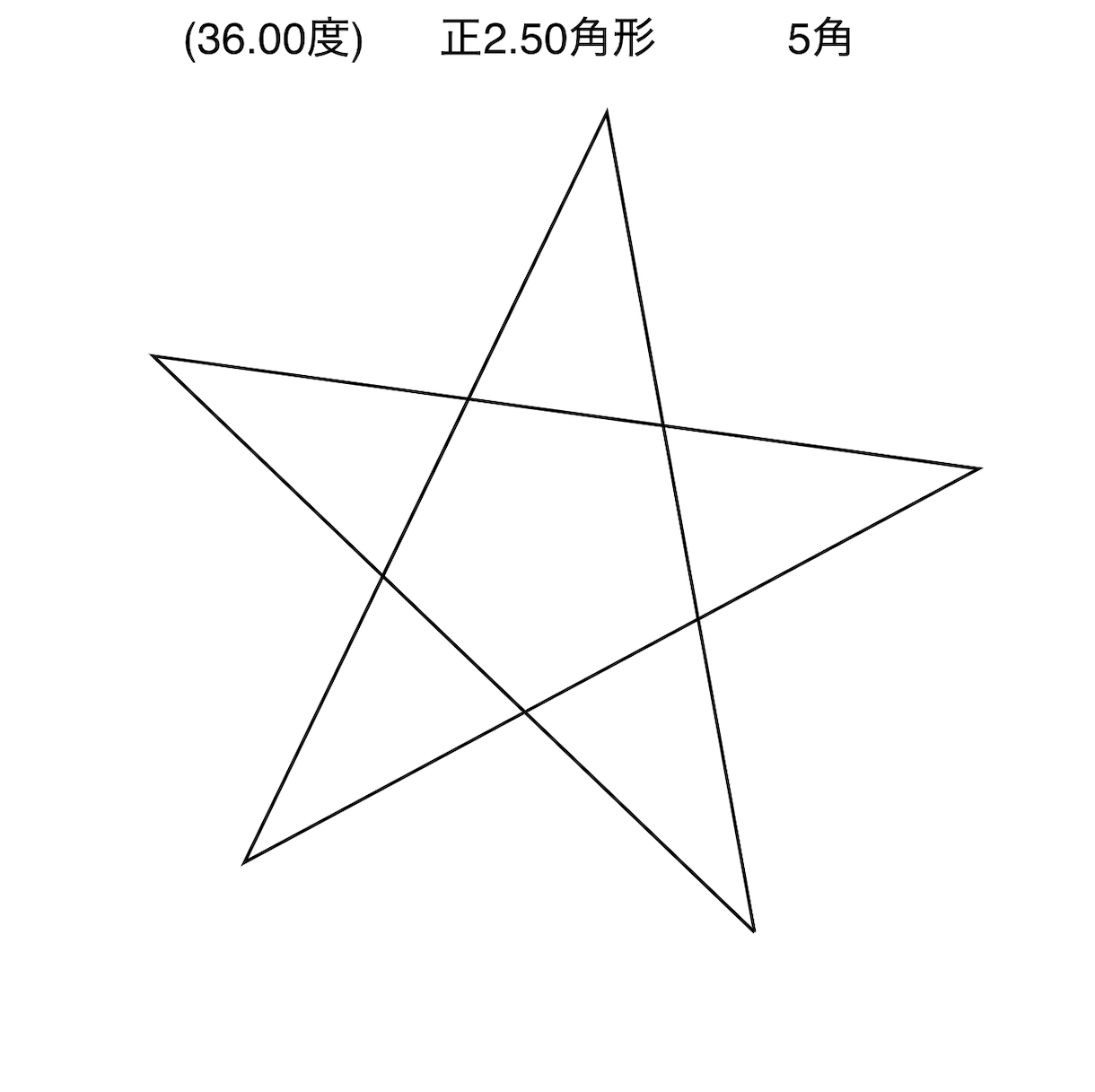



正2 22角形は何辺ある 正2 5角形の謎とvscodeでもf5 高専it系部活紹介レビュー Js Kosen 福野泰介の一日一創 Create Every Day By Taisuke Fukuno
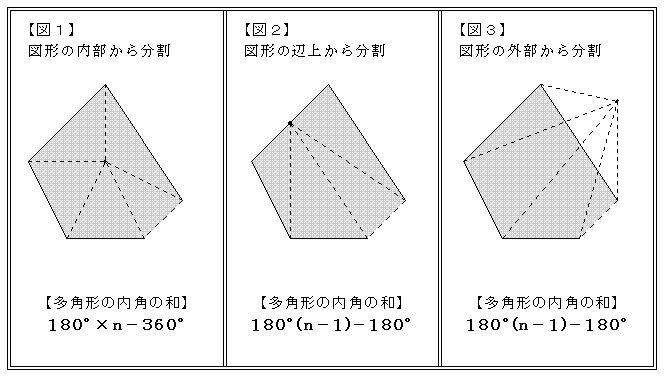
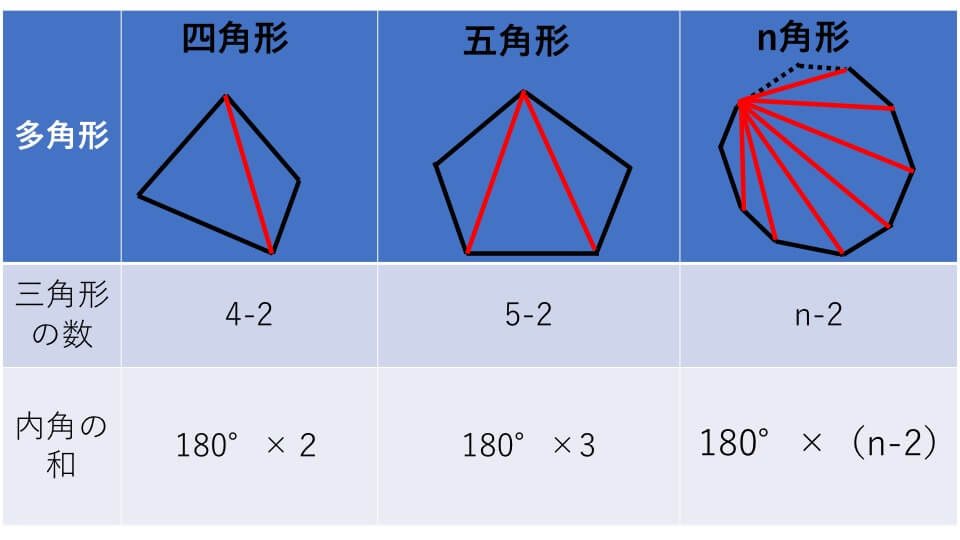
· 5角形 までの内角の 《円・半円・弧・扇形》の円周・面積の求め方と公式一覧|小学生の算数 円に関係する公式4種類をまとめました。 重要な公式なので確実に覚えるようにしましょう上の事実は次のように説明できます. まず, 多角形の各頂点における内角と一つの外角の和は常に 180° 180 ° なので, n n 角形の内角と外角の和の合計は, 180°×n 180 ° × n です.そして, n n 角形の外角の和は,これから内角の和をひいたものなので, 180三角形の数で内角の和が計算できます 五角形と六角形の内部に作成できる「三角形の数」「内角の和」は下の図の通り。 四角形と同じように、三角形の数が分かれば内角の和は求められますよね^^ どうですか? ここまではそれほど難しくないと思います。 多角形と言っても、まだまだ五角形、六角形と数が少ない形ですからね。 ということで! ここで一気に
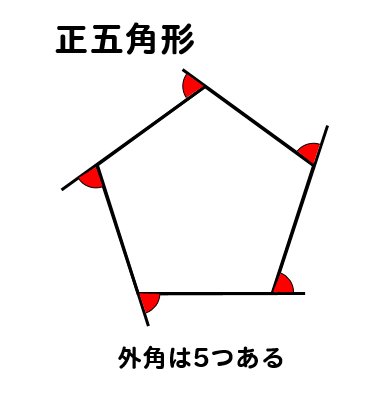



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




角度を計算する方法 9 ステップ 画像あり Wikihow




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
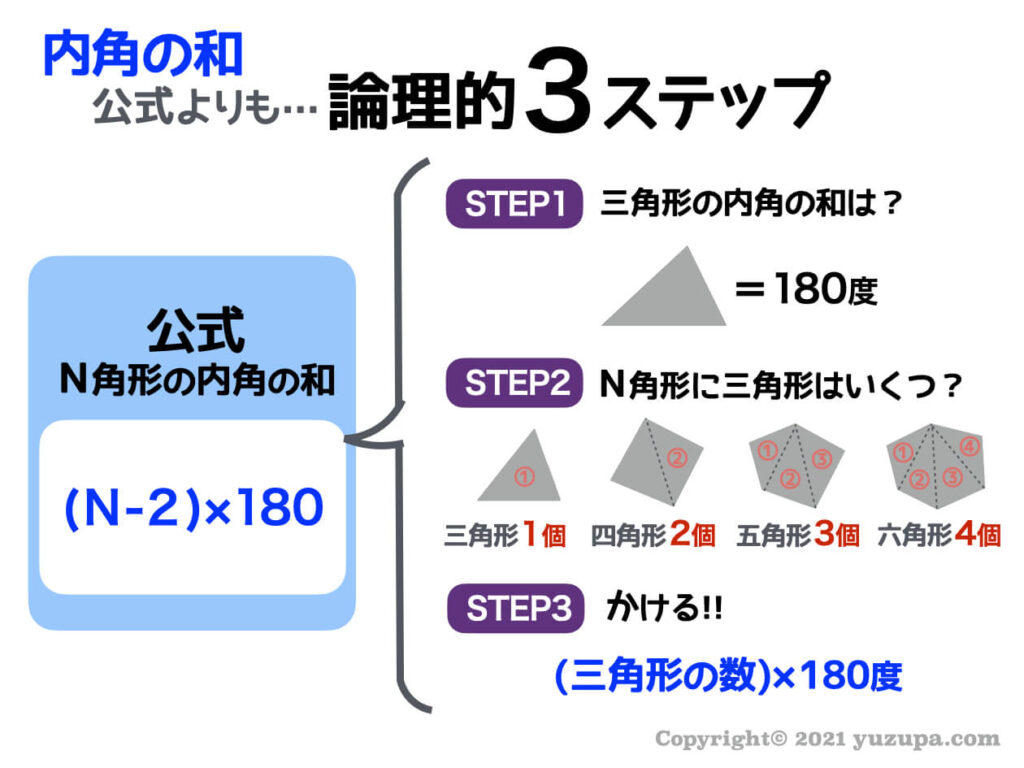



中学受験 多角形の内角の和 公式を忘れなくする論理的3ステップ かるび勉強部屋



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




内角の和 算数用語集



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋



1




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




分かりません 教えてください Clear



1




小学校5年 算数 正多角形の角の大きさ Youtube



多角形の内角の和は 1分でわかる公式 問題の求め方 簡単な証明



角度を求める 凸型多角形 Next Stageのブログ




最高三角形 角度 求め方 中学 最高のぬりえ
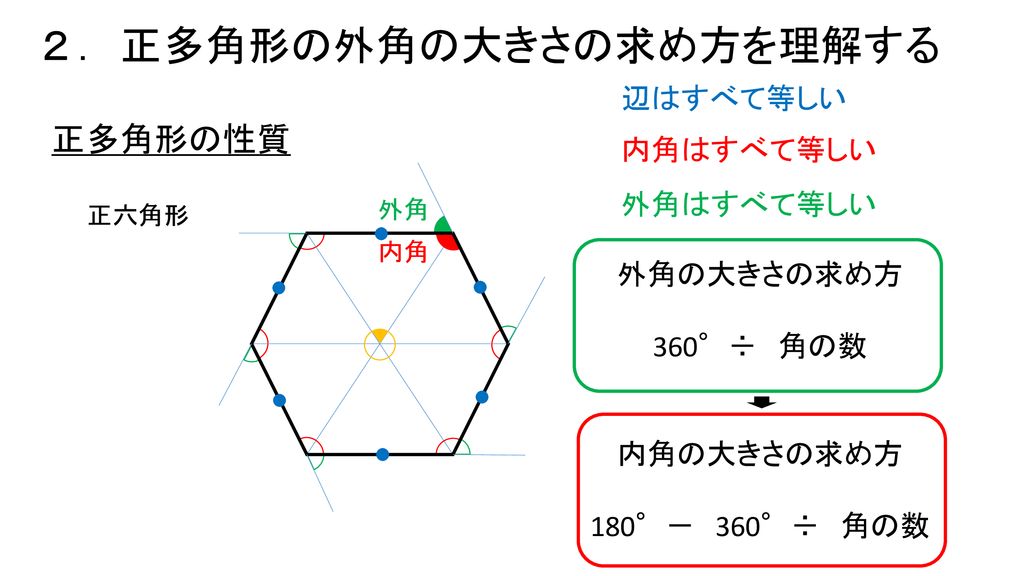



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download




ボード 学習ノート のピン
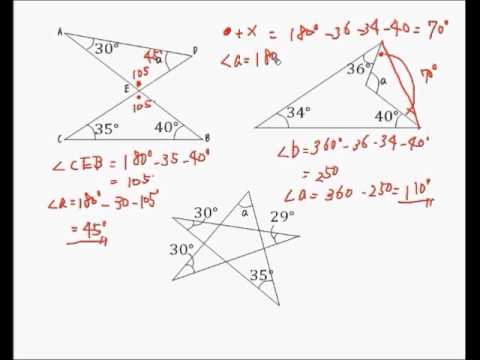



多角形から角を求める Youtube




小5 算数 小5 31 三角形の角 Youtube




いろいろな正多角形をかいてみよう 家庭学習レシピ




図形 角度の求め方 中2 画像の図形の内角の和は900度なのですが 求め Okwave




多角形の角度の和の求め方 添付画像の黒い印の角の角度の和を求めたいのです Okwave




課題学習の指導 数学



中2の数学の多角形の問題で この図形のyの角度の求め方を教えてください Yahoo 知恵袋




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




多角形の内角の和 算数の公式覚えてますか




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




正多角形の内角と外角の大きさ 具体例で学ぶ数学




円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ
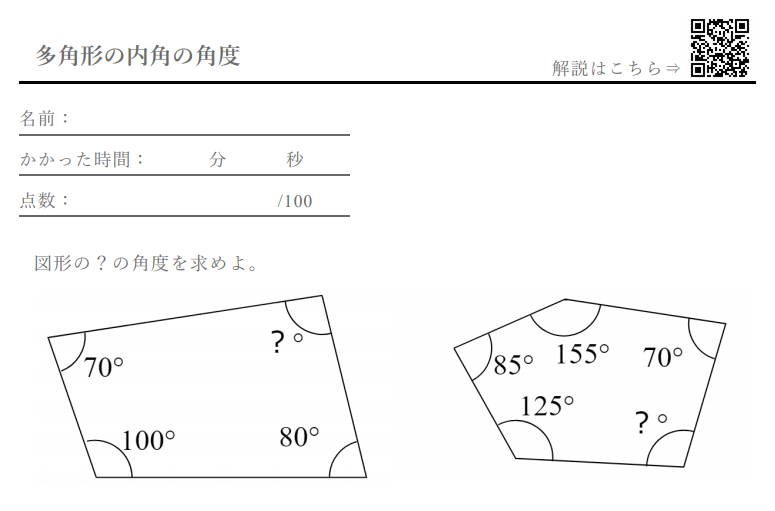



多角形 の内角の角度 計算ドリル 問題集 数学fun




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ



課題学習の指導 数学




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




8 2 Descubre Como Resolverlo En Qanda




中2数学 多角形の角度を求める公式と練習問題 Atstudier




星形の角度 内角の和の求め方を問題解説 数スタ




Bar2 1 1 Descubre Como Resolverlo En Qanda
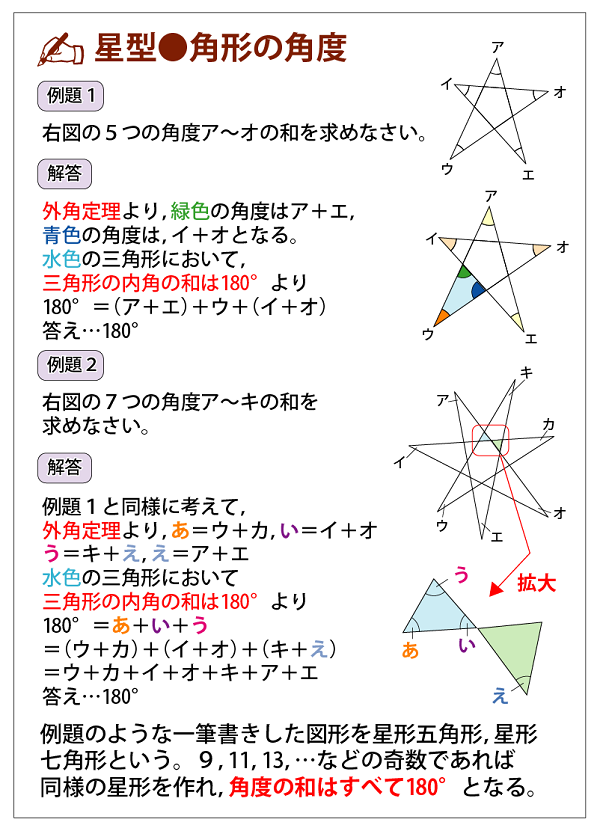



星型 角形の角度の問題 恋する中学受験 大学受験を見据えた中学受験



多角形の角




多角形の内角の和 は何度なのか を説明します おかわりドリル



Studydoctor多角形の角度の問題 中2数学 Studydoctor



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
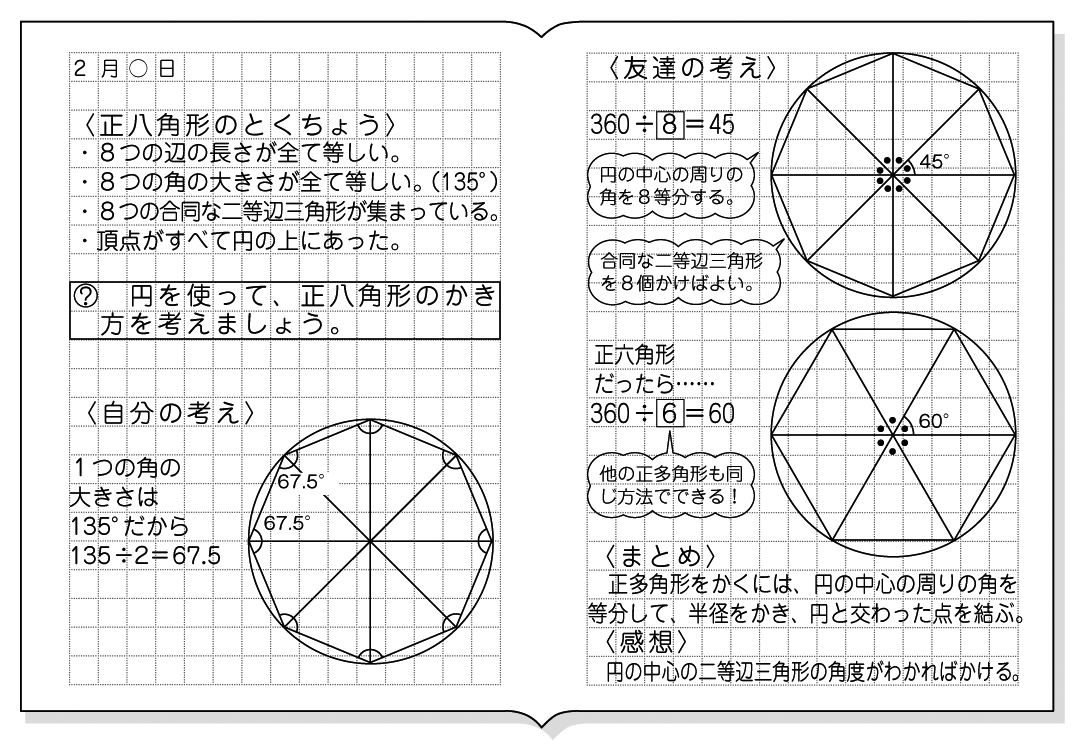



小5算数 正多角形と円 指導アイデア みんなの教育技術
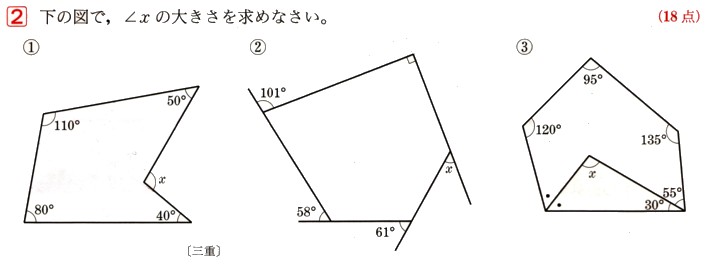



中学2年数学 図形の調べ方 三角形 多角形と角 確認問題2 解答 あんのん塾



1




中2数学 ブーメラン型角度の求め方を解説 数スタ
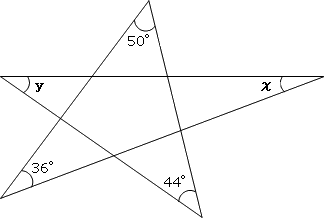



角度の求め方 算数の教え上手 学びの場 Com




内角の和 180 N 2 外角の和 360 教遊者
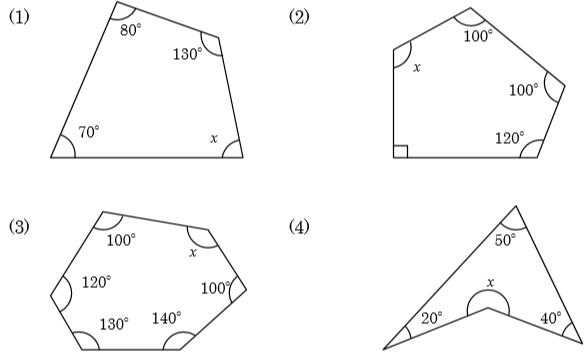



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu




内角の和 180 N 2 外角の和 360 教遊者
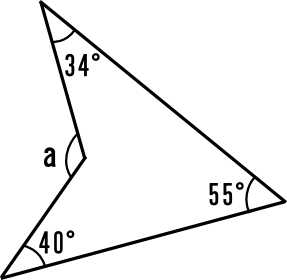



中学2年数学練習問題 図形の調べ方 多角形の内角と外角



Http Fzk Ed Shizuoka Ac Jp Shizuchu Wp Content Uploads Sites 4 17 02 5b4511dfa47fa1a398d0591ccee2 Pdf



問題1 平行線に二本の直線が交わっているとき Xの大きさを求めよう




図形の調べ方 N角形について 内角の和を求める 苦手な数学を簡単に



多角形の内角と外角 思考力を鍛える数学
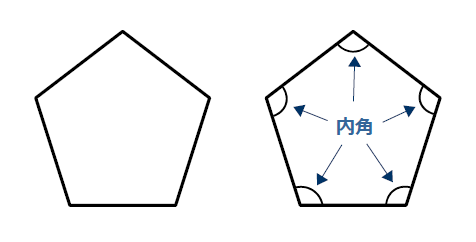



内角 ゆるゆるプログラミング
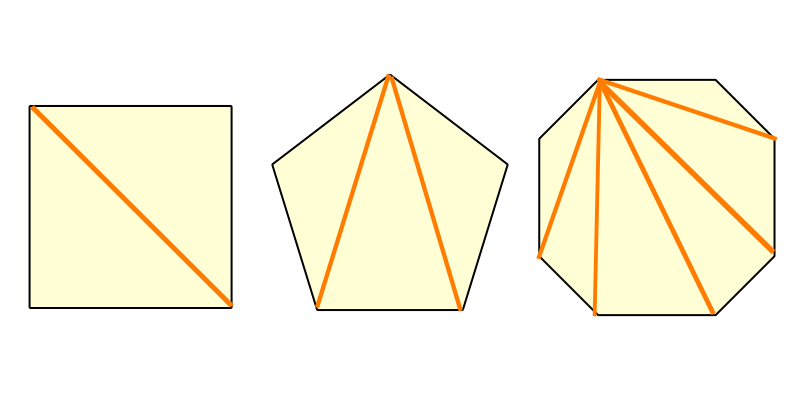



多角形の内角の和 簡単に計算できる電卓サイト




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題



Q Tbn And9gcqlnztwxojvc2bxd Jka7zv6jbk Xsvc6x 85lxfc78pht09gza Usqp Cau




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
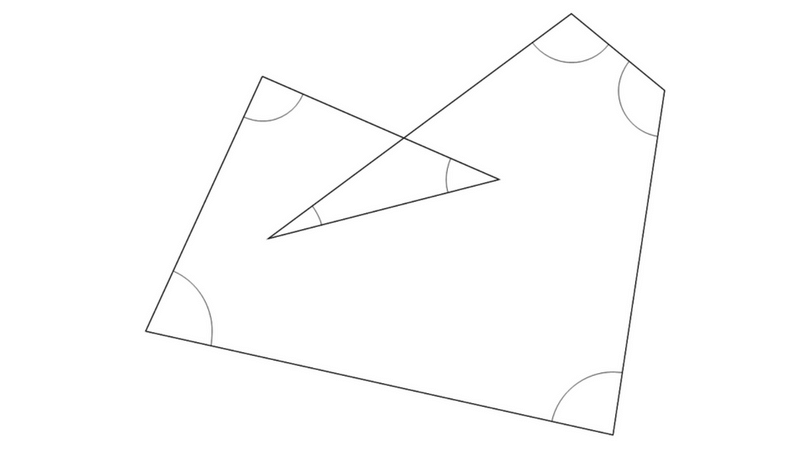



数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局
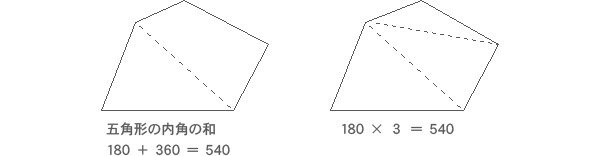



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版
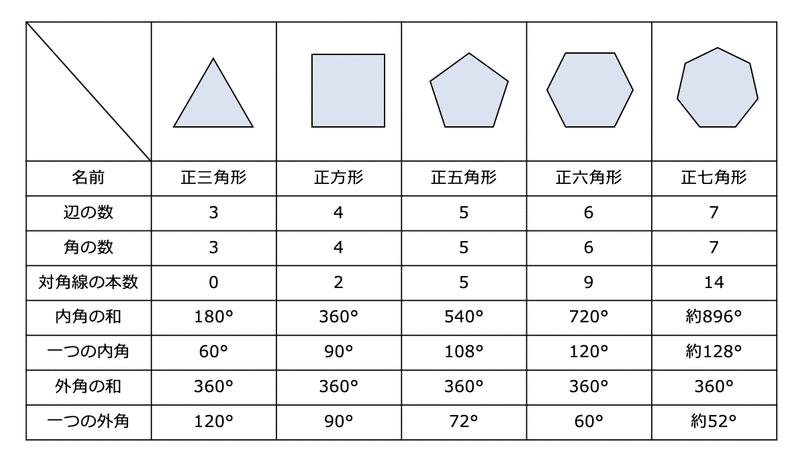



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の角度 添付した図形の Bgeの大きさを求めます 行き詰まっていま Okwave




多角形の角 無料で使える中学学習プリント




多角形の内角の和の公式と外角の和を利用した角度の求め方
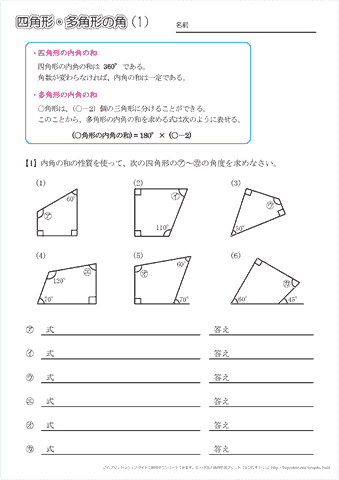



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




角度の求め方 算数の教え上手 学びの場 Com



小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報




多角形の内角の和 は何度なのか を説明します おかわりドリル
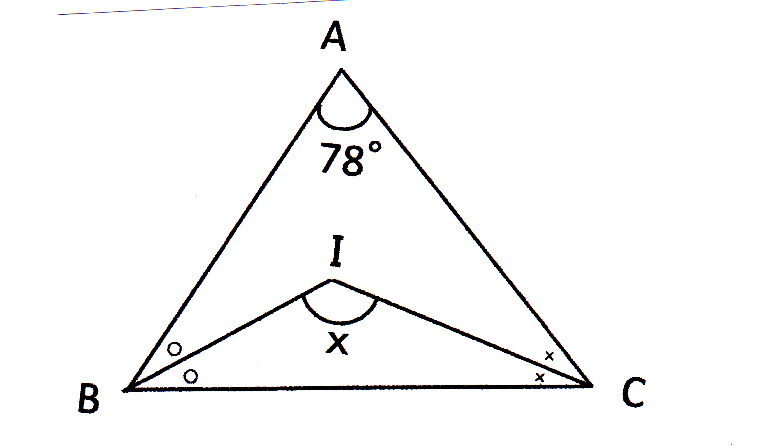



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方
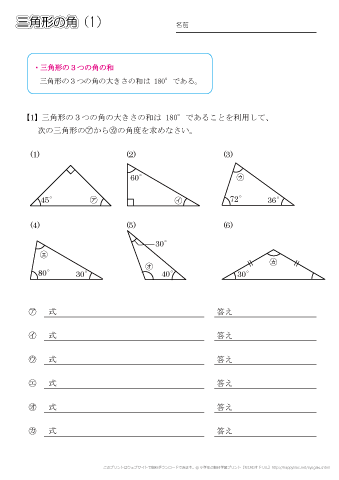



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear



720度 星形九角形の角度の和




多角形の内角の和 外角の和の公式 数学fun




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく
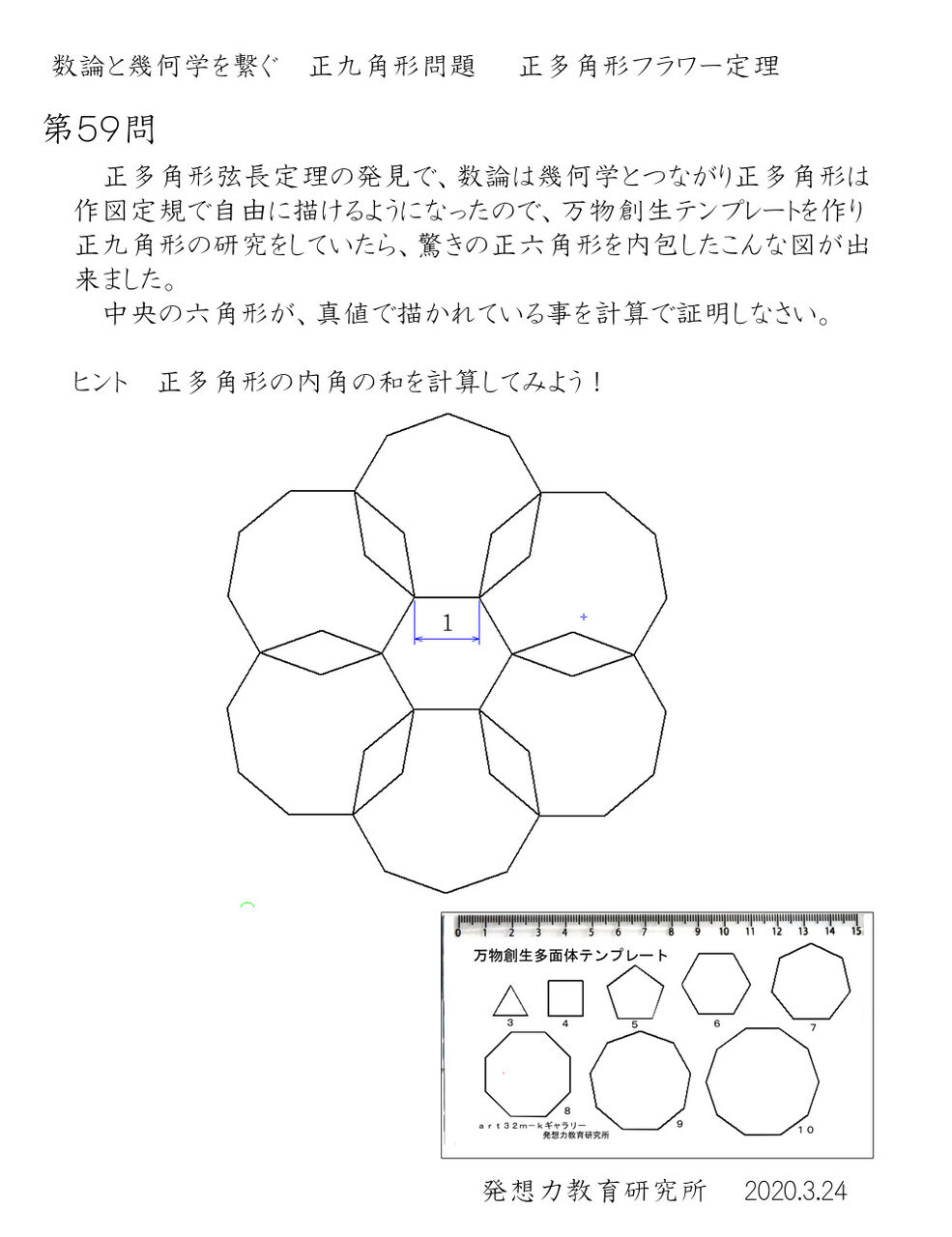



正9角形の証明問題 正多角形の間に存在する法則性を数論で証明する問題 発想力教育研究所 素数誕生のメカニズム




中2数学 複雑な多角形 角の和 応用問題




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿